Retornar para: Colunas - Fórum PCs
03/10/2005
< Computadores XI: Diagramas Lógicos >
Na coluna anterior, "Portas Lógicas", criamos a ponte entre o abstrato (lógica digital pura, álgebra Booleana) e o concreto (circuitos digitais em estado sólido que reproduzem o comportamento das expressões lógicas). Esta ponte é a "porta lógica", um circuito eletrônico cujo sinal de saída exprime o resultado da aplicação de uma operação da lógica digital sobre seus sinais de entrada.
As portas lógicas se situam no nível mais elementar da ciência da engenharia da computação. Elas são usadas como elementos básicos para a implementação de todo e qualquer circuito lógico de um computador. Seu estudo é fascinante, um dos raros casos em que uma teoria absolutamente abstrata pode ser imediatamente comprovada simplesmente implementando um circuito digital que reproduz a expressão algébrica correspondente. Infelizmente o estudo desta teoria está fora de nosso escopo, de modo que teremos que nos abster de discutir diversos aspectos teóricos, inclusive as interessantíssimas formas de simplificar expressões booleanas (por simplificação algébrica, mapas de Karnaugh ou tabelas de Quine-McKluskey) que permitem implementar circuitos aparentemente complicadíssimos combinando um número surpreendentemente pequeno de portas lógicas. Aqui vamos nos ater apenas aos aspectos essenciais que nos permitirão entender a forma pela qual os computadores se organizam internamente.
Mas, mesmo nesse nível elementar, precisaremos conhecer a simbologia gráfica e algébrica usada para representar as operações lógicas. Os símbolos estão representados na Figura 1. Note que a "negação" de uma porta é representada por um pequeno círculo no terminal de saída da porta correspondente (ou seja: as portas NAND e NOR são representadas pelo mesmo símbolo usado para as portas AND e OR ao qual se acrescentou um círculo no terminal de saída).

Figura 1: Símbolos gráficos e algébricos das portas lógicas
Uma propriedade interessante das portas lógicas é que elas podem ser implementadas através de combinações de outras portas lógicas simples. Nós mesmos já vimos um exemplo disso quando implementamos portas AND e OR acrescentando uma porta NOT à saída das portas NAND e NOR, respectivamente (se tem dúvidas, consulte os esquemas das duas últimas portas lógicas da coluna "Misturando transistores"). Isso traz uma conseqüência interessante: pode-se implementar qualquer porta lógica usando exclusivamente portas NOR ou portas NAND. Como essas são as de implementação mais simples (consulte novamente seus esquemas na coluna acima citada e veja porque), essa possibilidade simplifica bastante o projeto de circuitos digitais. Veja, na Figura 2, como é possível implementar as portas NOT, AND e OR combinando apenas portas NAND ou apenas portas NOR. Tem dúvidas? Pois faça um exercício: tente explicar para você mesmo porque as combinações fazem o efeito mostrado na figura. Se precisar, pegue lápis e papel e faça um esboço, verificando onde há corrente e onde não há.
Garanto que é um excelente exercício intelectual.
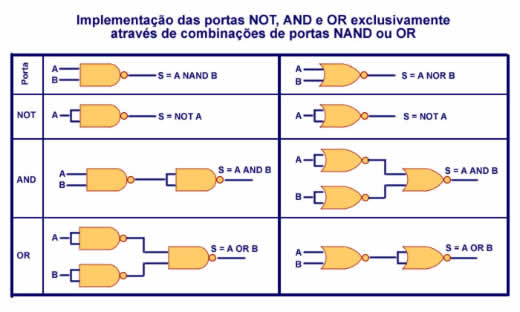
Figura 2: Combinações de portas simples
O uso dos símbolos simplifica muito o estudo dos circuitos digitais. Como cada circuito digital é a representação física de uma expressão da álgebra booleana, pode-se representar qualquer expressão algébrica (e, portanto, qualquer circuito digital) utilizando os símbolos das portas lógicas que formam o circuito, já que todo circuito digital é uma combinação de portas lógicas. Ao resultado disso (o gráfico criado com o uso dos símbolos) dá-se o nome de "diagrama lógico". Veja, na figura 3, o diagrama lógico do circuito que estudamos na coluna anterior, aquele equivalente à expressão S = (A OR B) AND (NOT C).
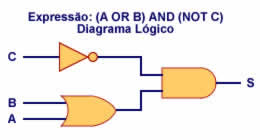
Figura 3: Diagrama lógico de circuito digital
Agora, que já conhecemos a simbologia gráfica e os diagramas lógicos, vamos abordar a última operação simples da lógica digital, a operação XOR ou "OU Exclusivo". Que ficou para o final porque é considerada "mais complicada" que as demais. Uma fama que, seguramente, ela não merece.
Pois acontece que as operações AND e OR, assim como a NOT, são muito fáceis de explicar usando fatos da vida diária. Frases como "posso entregar a encomenda a um OU outro irmão" ou "para ler o testamento é preciso que um E outro irmão estejam presentes" são facilmente entendidas como representações das operações lógicas OR e AND. E a operação NOT nada mais é que a negação de uma situação. Isso ajuda bastante a analisar os resultados de expressões que contêm tais operações. Mas e a XOR, ou "OU Exclusivo", por que tem fama de ser mais complicada?
A mim parece que esta fama deve-se apenas à má compreensão do sentido do adjetivo "exclusivo" usado no nome da operação. Um adjetivo que tem diversas acepções ("acepção" significa "cada um dos vários sentidos que palavras ou frases apresentam de acordo com cada contexto"; por exemplo: a palavra "ponto" tem acepções completamente diferentes quando se refere a pontuação, costura, geometria, geografia e assim por diante) Pense um pouco: o que você entende por "exclusivo"?
Na maioria das vezes o termo está associado às acepções "aquilo que é privado ou restrito" (como em "sala para uso exclusivo dos funcionários") ou que, "por privilégio, pertence a alguém" (como em "clube exclusivo"). Mas em geral nos esquecemos da acepção mais importante: "aquilo que exclui, que elimina, que tem poder para excluir" (todas as acepções citadas foram obtidas no dicionário Houaiss, versão eletrônica). Então "exclusivo" também é aquilo que exclui. E é justamente neste sentido que o adjetivo é usado para batizar a operação XOR.
Mas exclui como? Simples: pegue duas variáveis lógicas A e B e submeta-as à operação A XOR B. Imagine que A seja verdadeiro. Se assim é, para que o resultado seja verdadeiro, B NÃO PODE também ser verdadeiro. Agora, imagine o contrário: B é verdadeiro. Para que o resultado seja verdadeiro, A NÃO PODE também ser verdadeiro. Em suma: um exclui o outro (se um e verdadeiro, o outro não pode ser verdadeiro). Portanto, o resultado somente é verdadeiro se uma variável assumir o valor "verdadeiro" e a outra não (outra forma de dizer isso: o resultado somente é verdadeiro quando o valor das duas variáveis forem diferentes entre si, ou seja, um verdadeiro e outro falso, ou quando um excluir o outro – daí o nome "exclusivo").
Se você entendeu isso, fica fácil entender a tabela verdade da operação XOR mostrada na figura 4.
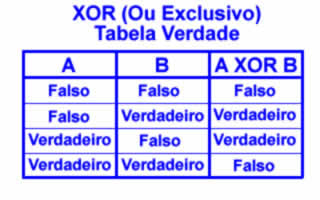
Figura 4: Tabela verdade da operação XOR
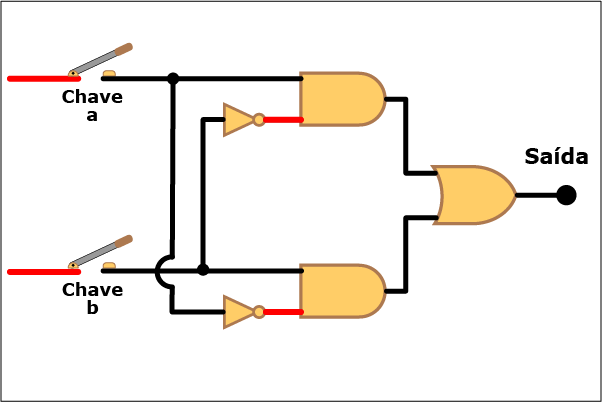
Mas como é que isso funciona na prática? Bem, vamos aproveitar essa pergunta para duas finalidades: mostrar o diagrama lógico do circuito que representa a operação e testar as diversas combinações de valores em uma animação. Veja, na Figura 5, o diagrama lógico e a tabela verdade de uma porta XOR, ou "OU Exclusivo".
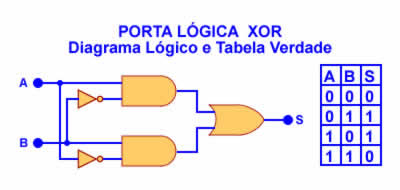
Figura 5: Porta XOR – Diagrama Lógico e Tabela Verdade
(Nesta figura inauguramos uma nova notação: se no cruzamento de duas linhas que representam condutores elétricos houver um pequeno círculo, os condutores estarão em contato um com o outro. Se não houver o círculo, não haverá contato).
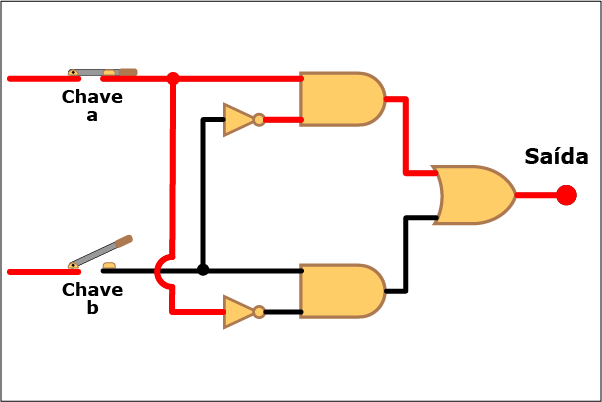
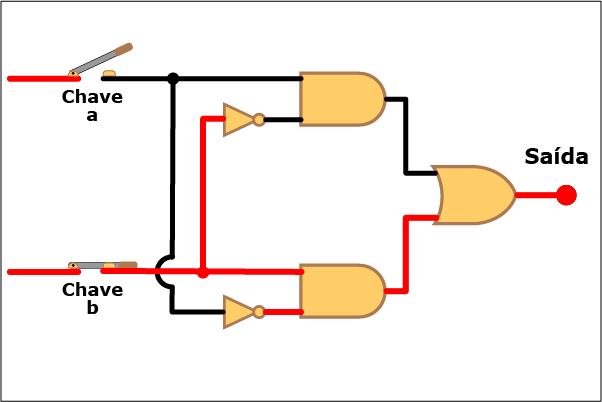
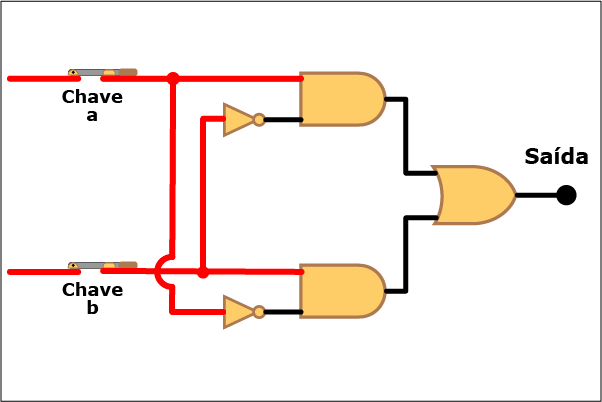
Conhecido o diagrama lógico, veja como o sistema funciona na Animação 1. Clique nos botões Liga e Desliga de cada chave para aplicar tensões nos terminais de entrada e repare o efeito disso na saída. Para ajudar a compreender o funcionamento da porta lógica, os condutores tornam-se vermelhos quando conduzem corrente.
Animação 1: Clique em Liga e Desliga para aplicar tensões nas entradas
Agora já dispomos das ferramentas necessárias para construir nossos circuitos digitais e, melhor, sabemos como usá-las. Nas próximas colunas veremos alguns circuitos elementares e interpretaremos seu funcionamento.