Sítio do Piropo

B. Piropo

< Coluna B. Piropo >
< (publicada no site "Fórum PCs") >

Na coluna anterior, "Diagramas Lógicos", discutimos a simbologia gráfica e algébrica usada para representar as operações lógicas, uma ferramenta essencial para que possamos analisar circuitos digitais. Agora que dispomos dela, poderemos usá-la para facilitar nossa jornada pelos caminhos da organização interna dos computadores.

Então vamos adiante.

Hoje em dia, por quaisquer dez merréis compra-se em um camelô uma máquina de calcular eletrônica capaz de efetuar as quatro operações elementares, raiz quadrada, elevar ao quadrado, calcular porcentagem e, de lambuja, oferece ainda uma memória para armazenar resultados. As primeiras, lançadas há cerca de trinta anos, faziam mais ou menos a mesma coisa e custavam quase mil dólares americanos.

Você já pensou em como é que uma maquineta daquelas consegue "fazer contas"? Como, usando apenas circuitos eletrônicos contendo portas lógicas, é possível efetuar cálculos? Que mistério é esse?

Mistério nenhum. Na verdade é uma singela combinação de circuitos que resulta nesse aparente milagre tecnológico. Uma combinação que se baseia nos circuitos "somadores", ou seja, que fazem somas. Como a multiplicação é uma sucessão de somas, tendo-se um circuito que some, fica fácil desenvolver um que multiplique. Ou que subtraia, já que a subtração é uma soma "ao contrário". Ou que divida, já que a divisão é o oposto da multiplicação. E assim por diante. Então, se conseguirmos desenvolver um circuito que seja capaz de somar usando portas lógicas, teremos a chave da questão.

Mas para entendermos um circuito capaz de somar precisamos, primeiro, aprender a somar.

Como? O nobre leitor ou briosa leitora já sabe somar desde criança? Ótimo. Então faça a seguinte soma:

(1001 + 0101) onde ambas as parcelas estão representadas em binário (ou seja, no sistema numérico posicional de base dois).

Ah, em binário é mais difícil? Pois é justamente isso que eu queria dizer com "aprender a somar" (não vale converter as parcelas para decimal, somá-las, e depois converter a soma para binário; o resultado, evidentemente, é o mesmo, mas seria ininteligível para um computador). Para entender como computadores somam, precisamos somar em binário. Então mãos à obra (os que já sabem alguma aritmética binária podem saltar este trecho e seguir diretamente para a descrição dos circuitos somadores).

Na verdade, a primeira impressão é enganosa. Pois somar em binário é MUITO mais fácil que em decimal. E se você acha que estou exagerando é apenas porque está acostumado a somar em decimal desde criancinha. Porque um raciocínio elementar prova que tenho razão: como o sistema binário usa apenas dois algarismos, o "zero" e o "um", só existem quatro combinações possíveis (além do "vai um" que veremos adiante): (0 + 0), (0 + 1), (1 + 0) e (1 + 1). Essa é toda a "taboada de somar" dos números binários (se é que ainda existe a velha "taboada" que fui obrigado a decorar no curso primário).

A soma (zero mais zero) dará sempre zero, seja qual for a base. Assim como, em toda base, somar (zero mais um) ou (um mais zero) dará sempre um. O problema começa quando somamos, em binário, (um mais um). Porque (1 + 1 = 2) e em binário não há algarismo para representar dois. Na verdade, em nenhum sistema numérico posicional existe um algarismo para representar a base.

Então, como representaremos "dois" em binário? Ora, do mesmo jeito que representamos a base em qualquer sistema numérico posicional: movendo o "um" uma "casa" para a esquerda e acrescentando um "zero' à sua direita. Em decimal, isso dá "10" que vale dez. Mas notou que o "10" está entre aspas? Isso porque ele só representa "dez" em decimal. Na base oito, "10" representa oito, o valor da base. Na base dezesseis, "10" representa dezesseis; na base vinte, "10" representa vinte e assim por diante. Portanto, na base dois, "10" só pode representar dois. Logo, em binário: (1 + 1 = 10). E resista à tentação de ler isso que está entre parênteses como "um mais um é igual a dez". Não é. Lembre-se que tudo ali está em binário, portanto deve ser lido "um mais um é igual a dois", como em qualquer outra base. Afinal, se tem uma coisa que sabemos desde criancinha é que um mais um é igual a dois.

Então, somando parcelas algarismo a algarismo (ou bit a bit, já que um bit é justamente um "binary digit", ou algarismo binário), sempre na mesma coluna ou "casa", a coisa fica como mostrado na Figura 1:

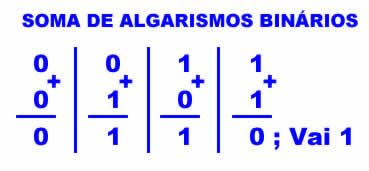
Figura 1: Soma de dígitos binários (bits)

Mas que diabos significa esse "Vai 1"?

Ora, a mesma coisa que na soma de decimais. Quando a soma de dois algarismos que estão na mesma posição (ou "casa") decimal resulta em um valor igual ou superior à base (no caso, dez), colocamos no resultado o que "sobra" de dez e somamos uma unidade à posição imediatamente superior. Veja um exemplo na Figura 2.

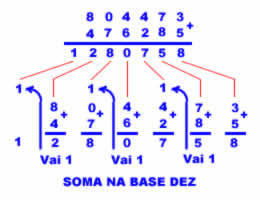
Figura 2: Soma na base dez

O algoritmo para somar números expressos em sistemas numéricos posicionais é sempre o mesmo: coloca-se os números um acima do outro, alinhados pela direita, ou seja, com as posições correspondentes aos algarismos menos significativos de cada parcela diretamente acima uma da outra e soma-se os algarismos, "casa" a "casa", ou seja, coluna a coluna, da direita para a esquerda. Sempre que a soma de dois algarismos ultrapassar o valor da base (dez, no caso do exemplo da Figura 2), anota-se na soma o valor do resto e soma-se uma unidade à casa vizinha da esquerda (o popular "vai um").

Antes de prosseguir, um lembrete importante: acostumemo-nos a numerar as posições, ou "casas" da direita para a esquerda a partir de zero. A posição de ordem 0 é a da extremidade direita, correspondente ao algarismo menos significativo. Portanto a de ordem 1 é a segunda a partir da direita e assim por diante.

Agora, voltemos ao assunto do "Vai 1". No exemplo da Figura 2 ele ocorreu na casa de ordem 1, onde (7 + 8 = 15; resto 5), na de ordem 3, onde (6 + 4 = 10; resto zero) e na de ordem 5 (8 + 4 = 12; resto 2). Note que o último "vai um", o da casa de ordem mais alta, a de ordem 5, foi simplesmente acrescentado à esquerda da soma, já que não havia nada com que somá-lo na casa de ordem 6.

Agora, apliquemos o mesmo algoritmo para somas em binário, ou seja, na base dois. Veja dois exemplos na Figura 3, o da esquerda mais simples, o da direita um pouco mais complicado (já veremos o porquê dessa complicação).

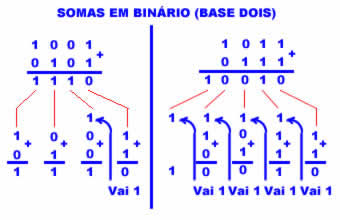
Figura 3: Soma na base dois

Examine primeiro a soma da esquerda, (1001 + 0101 = 1110). Note que o algoritmo é o mesmo usado para a soma em decimal: soma-se os dois algarismos (no caso, os dois "bits", ou dígitos binários, já que os números são expressos em binário) em cada "casa" ou coluna da mesma ordem a partir da direita, ou seja, começando pela coluna de ordem zero, correspondente ao algarismo menos significativo. Note que na coluna de ordem 0 do exemplo da esquerda temos (1 + 1 = 0; Vai 1), pois a soma "um mais um" é igual a dois e dois é a base. Esse "um" que "vai" é somado com os dois zeros da casa de ordem 1 (a segunda a partir da esquerda), ficando: ("Vem 1" + 0 + 0 = 1). Continue repetindo o algoritmo, coluna a coluna, e veja o resultado se formar.

Agora repare na soma do exemplo da direita. O "complicador" está na coluna de ordem 1, a segunda a partir da esquerda. Ela representa a soma de (1 + 1) à qual se deve acrescentar uma unidade devido ao "Vai 1" da coluna de ordem zero. Então, proceda assim: primeiro, some o "Vem 1" com o primeiro bit 1 e chegue ao resultado parcial ("Vem 1" + 1 = 0; Vai um). Pegue esse um do "Vai 1" e passe para cima da coluna de ordem 2. Agora, some o "0" do resultado parcial com o segundo bit 1, o que resulta em (0 + 1 = 1). Escreva esse "um" no resultado e prossiga. Parece complicado, mas se você treinar um pouco verá que é de uma simplicidade franciscana. Para quem, como você, acostumou-se a somar números expressos na base dez, somar na base dois é moleza.

Agora, que já sabemos somar, vamos aos circuitos somadores.

A primeira coisa que temos que considerar é que a coluna mais fácil de somar é a coluna (ou "casa") de ordem zero, a que corresponde aos algarismos menos significativos. E a razão é simples: como ela é sempre a primeira a ser somada, para ela nunca "Vem 1", já que não há coluna alguma antes dela. Então, se construirmos a tabela dos valores possíveis para a soma de dois bits da coluna de ordem zero teremos o resultado exibido na Figura 4.

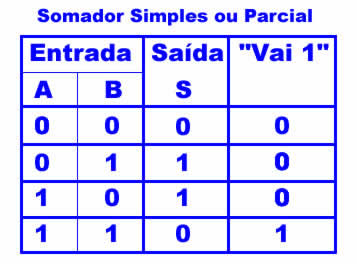
Figura 4: Tabela de um somador simples

O circuito, então, deverá ter duas entradas, A e B, correspondentes aos bits a serem somados, e duas saídas, S (correspondente à soma dos bits A e B) e "Vai 1", um bit a ser acrescentado à próxima coluna quando o resultado da soma for igual à base (dois, no caso). O diagrama lógico deste circuito é mostrado na Figura 5.

Como ele apenas é usado para somar os bits menos significativos, ou seja, os da coluna de ordem zero, as entradas estão assinaladas como Ao e Bo.

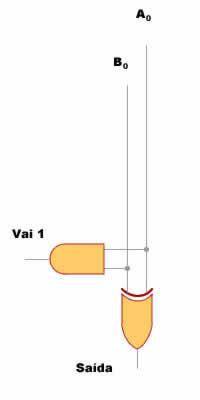
Figura 5: Diagrama lógico de um circuito somador parcial

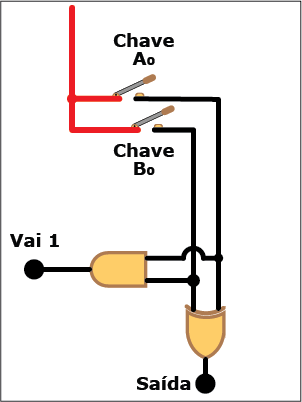
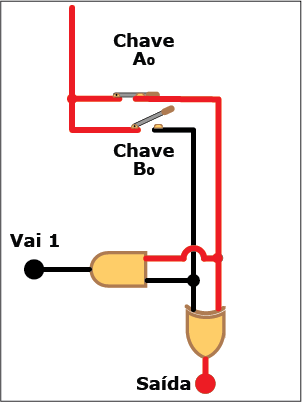
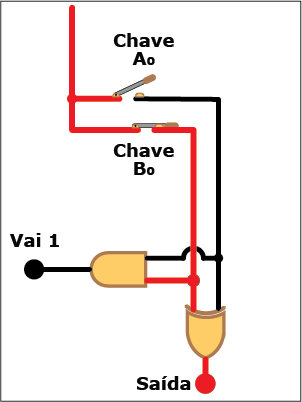
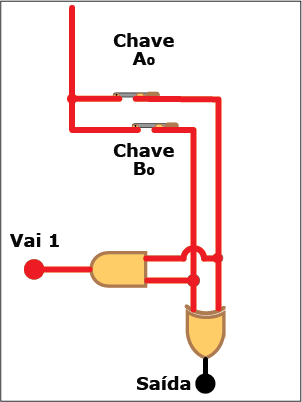
Como você vê, somar dois bits é mais simples do que parecia. Basta combinar duas portas lógicas, uma XOR e uma AND, e o problema está resolvido. Verifique, na Animação 1, como a coisa funciona. Clique nos botões "Liga" e "Desliga" para "ligar", ou atribuir o valor "um", e "desligar", ou atribuir o valor "zero" aos bits Ao e Bo da entrada e veja como isso se reflete nos valores da saída e do "Vai 1". Mas não se limite a observar os indicadores acenderem e apagarem: acompanhe, com os conhecimentos sobre portas lógicas e suas tabelas verdade, os trechos energizados (em vermelho) e não energizados (em preto) de cada estado do circuito e procure entender porque eles estão nestes estados (se precisar refrescar a memória, consulte as colunas anteriores desta série). Garanto que é um bom exercício mental.

ANIMAÇÃO 1: CLIQUE NOS BOTÕES "LIGAR" E "DESLIGAR" PARA VERIFICAR O FUNCIONAMENTO DO CIRCUITO DO SOMADOR PARCIAL

Mas como somar os demais bits de um número, aqueles nas posições (ou "casas") de ordem maior que 0? O complicador, naturalmente, decorre do fato de ser necessário saber se "Veio 1" ou não da soma dos bits da posição anterior. O circuito terá então três entradas: os bits A e B a serem somados e o eventual "Vem 1" da posição de ordem imediatamente inferior. E duas saídas, S, o resultado da soma, e o "Vai 1" caso a soma iguale ou exceda o valor da base. As combinações de valores são as representadas pela Tabela da Figura 7.

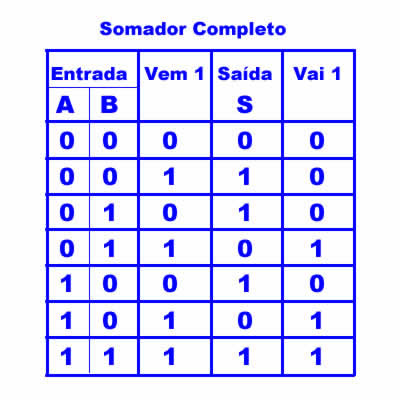
Figura 7: Tabela de um somador completo

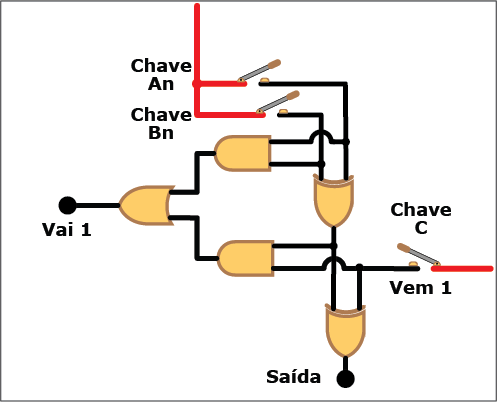
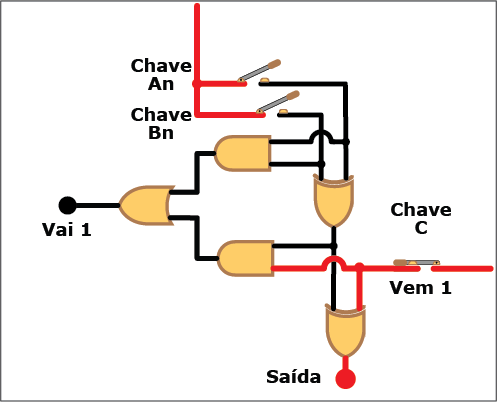
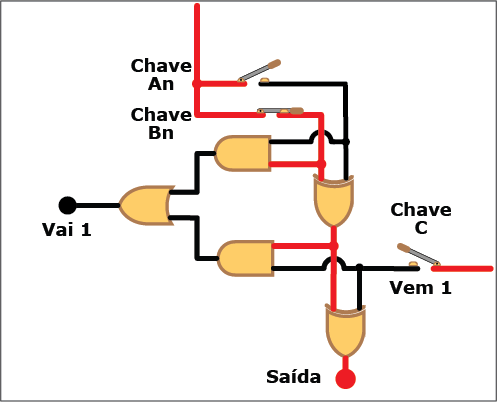
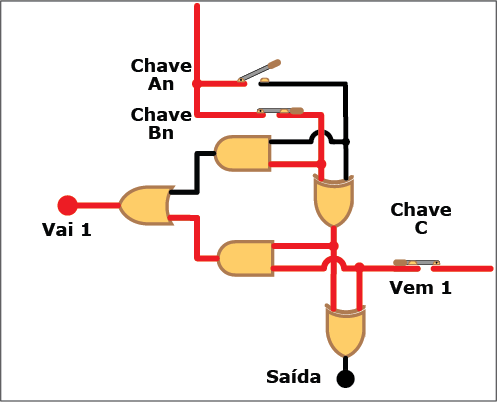
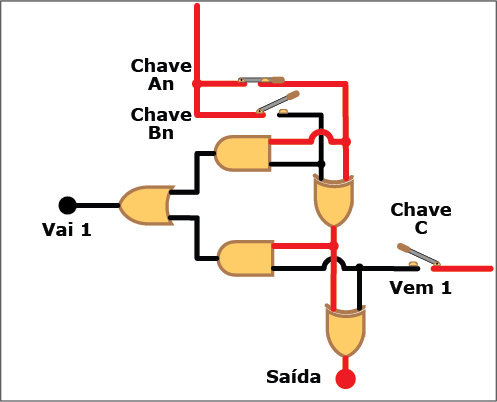
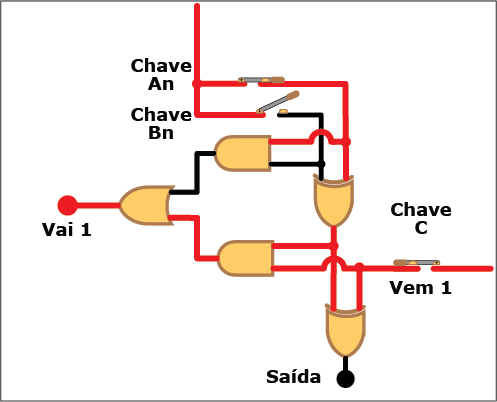
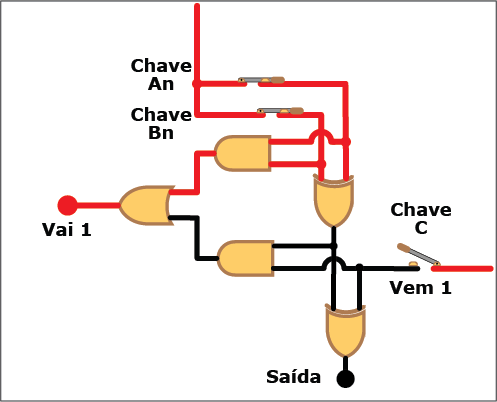
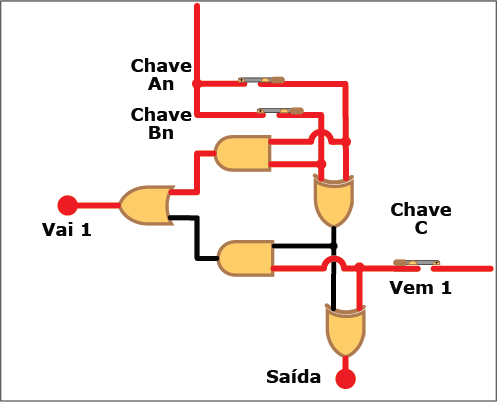
A Figura 8 mostra o diagrama lógico do circuito correspondente, com as entradas An, Bn (os bits a serem somados) e "Vem 1" (de um eventual "Vai 1" da coluna de ordem imediatamente inferior), e duas saídas: S, (a soma dos bits An, Bn e "Vem 1"), e "Vai 1" (o bit a ser acrescentado à próxima coluna quando o resultado da soma for igual ou superior à base).

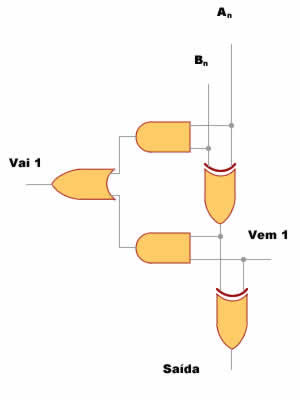
Figura 8: Diagrama lógico de um circuito somador completo

Também neste caso, apesar da complicação adicional trazida pelo "Vem 1", somar dois bits continua sendo uma tarefa simples. O número de portas lógicas a serem combinadas agora são cinco, duas XOR, duas AND e uma OR. Também nesse caso você pode verificar na Animação 2 como a coisa funciona. Clique nos botões para "ligar" (ou atribuir o valor "um") e "desligar" (ou atribuir o valor "zero") aos bits An, Bn e "Vem 1" e veja como isso se reflete nos valores da saída e do "Vai 1". Mas, novamente, não se limite a observar os circutos se energigarem e desenergizarem: acompanhe, com os conhecimentos sobre portas lógicas e suas tabelas verdade, os trechos energizados (em vermelho) e não energizados (em preto) de cada estado do circuito.

ANIMAÇÃO 2: CLIQUE NOS BOTÕES "LIGAR" E "DESLIGAR" PARA VERIFICAR O FUNCIONAMENTO DO CIRCUITO DO SOMADOR COMPLETO

Agora que sabemos como funcionam os somadores parcial e completo, fica fácil combiná-los para somar dois números de dois bits cada. Os bits menos significativos (de ordem 0) são somados usando um circuito somador parcial e os bits de ordem imediatamente superior (ordem 1) precisam utilizar um somador completo devido à possibilidade de "vir 1" da soma dos bits menos significativos. A Figura 10 mostra o diagrama lógico deste circuito.

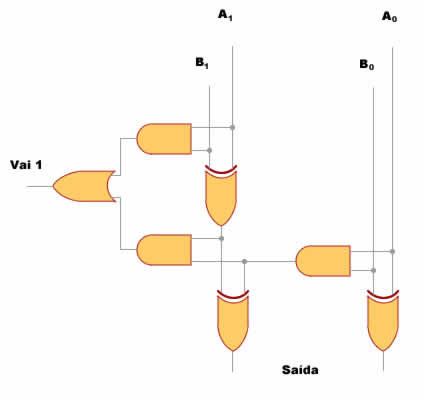
Figura 10: Diagrama lógico de um circuito somador de dois bits

Repare como a coisa é simples. Imagine que os números sejam ordenados um acima do outro, de forma que os bits menos significativos fiquem um sobre o outro, no caso Ao e Bo, somados pelo somador parcial à direita da figura. Veja que o "Vai 1" desta soma é encaminhado diretamente (como entrada "Vem 1") ao somador completo, à esquerda. Os bits dos resultados das somas das duas colunas são mostrados em baixo, na saída. Caso haja um "estouro" (o resultado não couber em um número de dois bits, ou seja, se for maior que três) isso se refletirá na saída "Vai 1" à esquerda, que assumirá o valor "um".

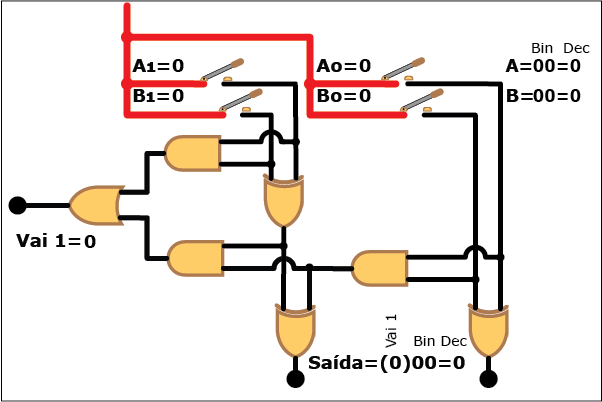
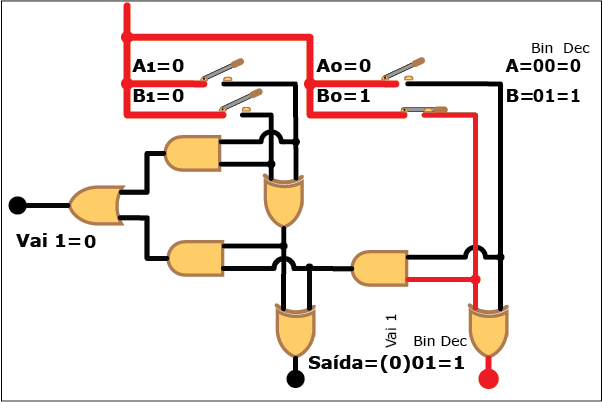
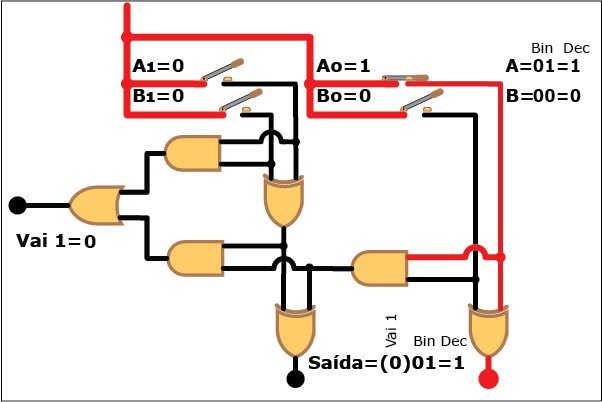
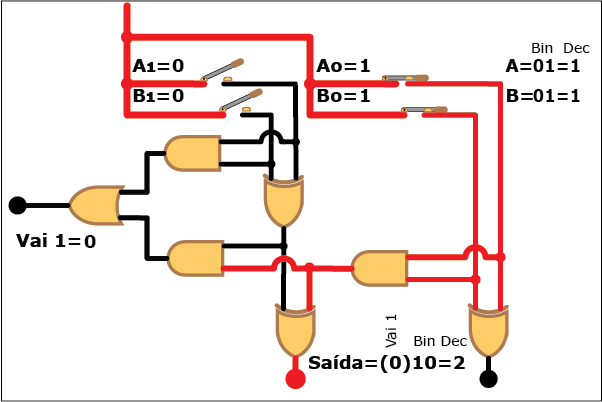
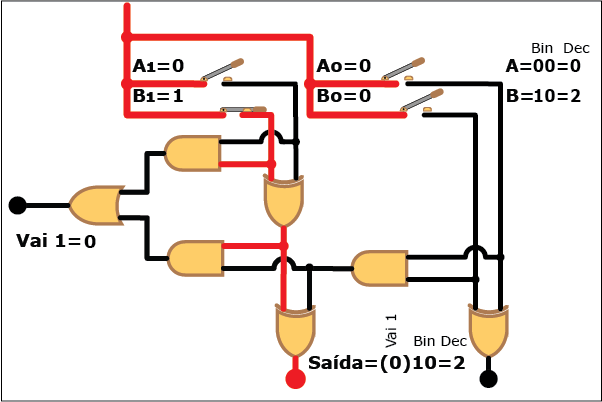
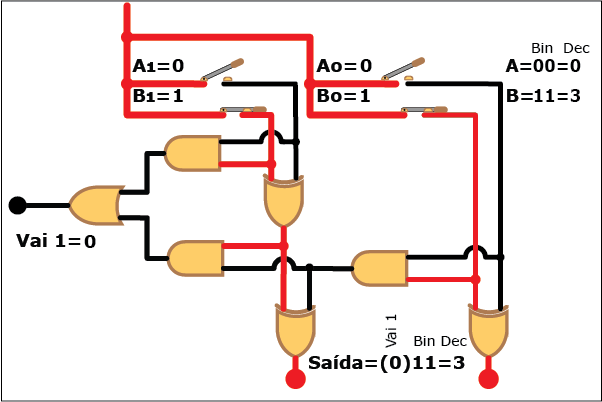
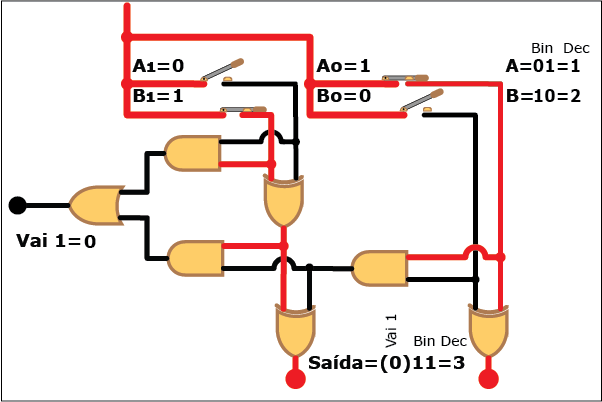
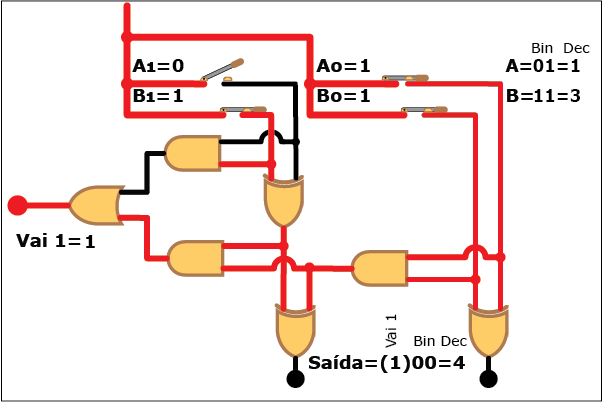
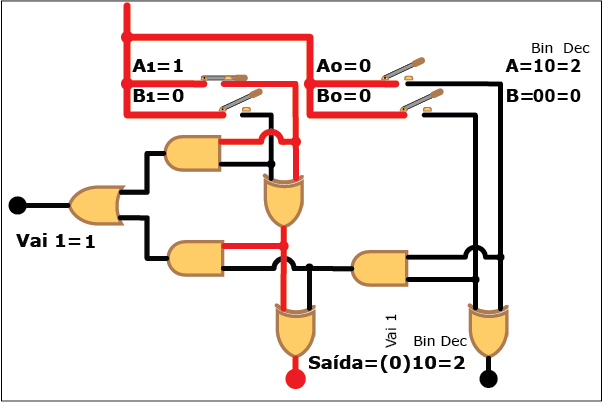
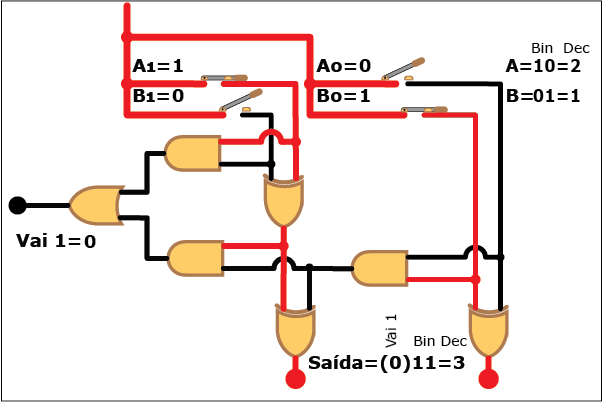
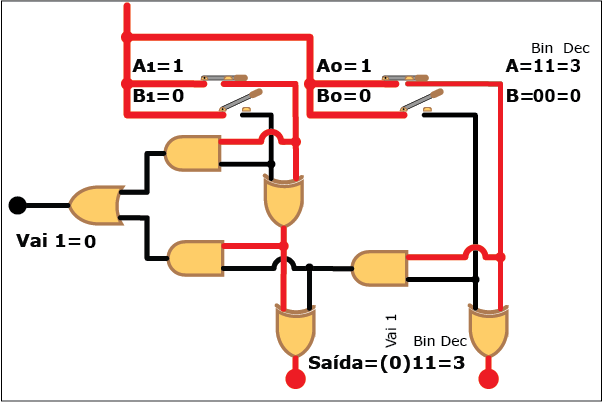
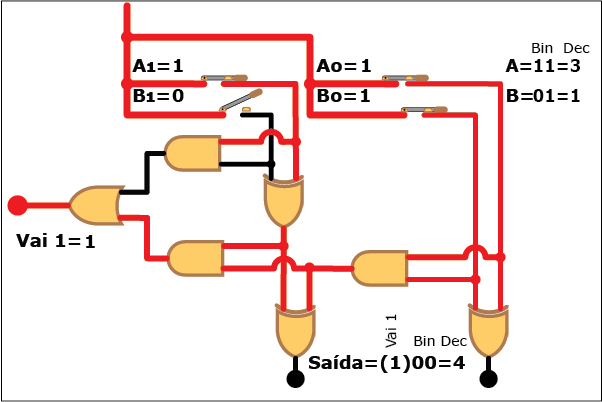
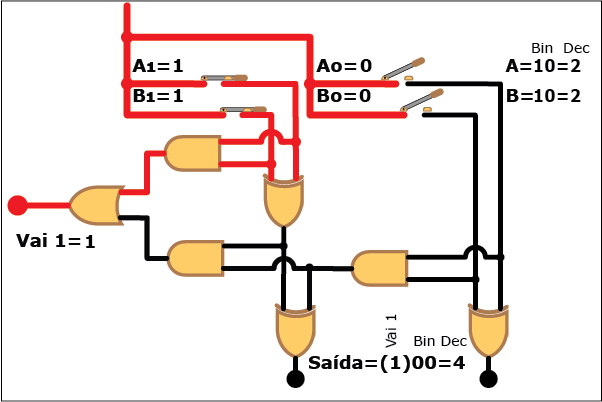
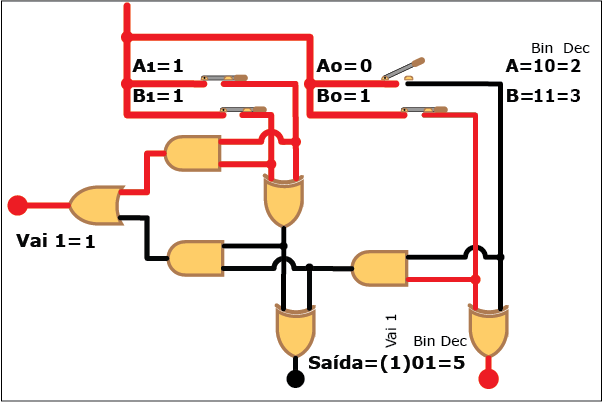
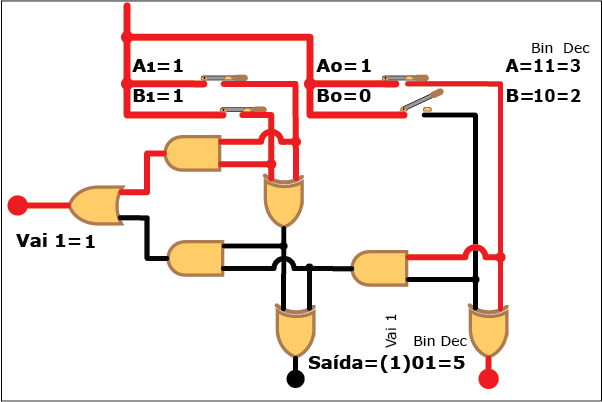
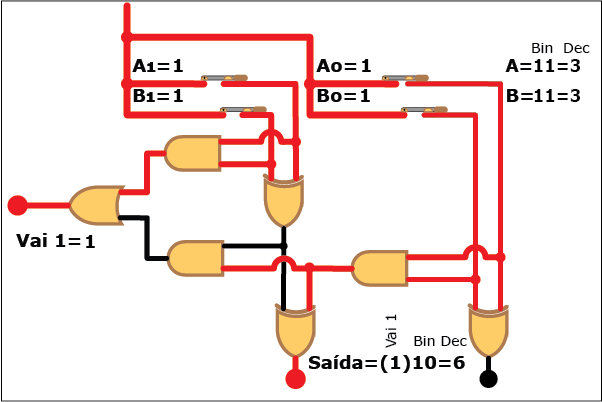
Veja como este circuito funciona na Animação 3. Altere os valores das parcelas clicando sobre os botões "Desliga" e "Liga" para atribuir valores "zero" e "um" a cada bit das parcelas A e B (os valores resultantes são mostrados em binário e decimal á direita da figura, tanto para A e B quanto para a soma S; neste último caso, quando o valor da soma exceder a três, ou seja, quando a saída "Vai 1" estiver ativa, o bit "1" correspondente é mostrado entre parênteses à esquerda dos dois bits da soma). Repare como, apesar da aparente complexidade, somar dois números é uma tarefa relativamente simples com o uso de circuitos digitais que empregam portas lógicas.

ANIMAÇÃO 3: CLIQUE NOS BOTÕES "LIGAR" E "DESLIGAR" PARA VERIFICAR O FUNCIONAMENTO DO CIRCUITO DO SOMADOR DE DOIS BITS

Os valores possíveis de números de dois bits vão de zero a quatro. O número total de combinações de somas é de dezesseis (4 x 4 = 16). Já um circuito somador de duas parcelas de oito bits cada resultaria em somas de dois números que variam de zero a 255 e a combinação de todas as parcelas possíveis atingiria a 65.536 (256 x 256). O circuito não é muito complicado, mas resultaria em um emaranhado de ligações que acabaria dificultando a compreensão. Mas, para facilitar o entendimento e mostrar como pode-se combinar qualquer número de somadores, abaixo vocês verão o diagrama lógico de um circuito capaz de somar duas parcelas de quatro bits cada. Fico devendo a animação, pois o número de total de combinações chegaria a 256 e não me imagino criando uma animação com 256 quadros. Mas o diagrama lógico está aqui na Figura 12:

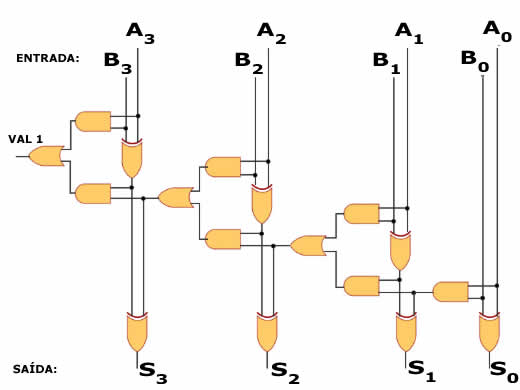
Figura 12: Diagrama lógico de um circuito somador de quatro bits

Como você vê, não há mistério nos circuitos digitais. Basta um pouco de paciência para entendê-los. Isso que está aí em cima é o diagrama lógico de um dispositivo capaz de efetuar somas de duas parcelas de quatro bits cada (ou seja, de dois números menores que 16). Uma somazinha besta, naturalmente, que qualquer criança pode fazer "de cabeça". Mas o importante não é o tamanho das parcelas, o importante é o funcionamento do circuito. Se você entendeu como ele funciona, entenderá o funcionamento de um circuito capaz de fazer somas de parcelas de qualquer tamanho, já que basta continuar combinando circuitos somadores bit a bit para aumentar o tamanho das parcelas.

E se você entendeu como somar, entenderá como subtrair, multiplicar e dividir, já que como vimos todas essas operações são baseadas na soma.

Em resumo, hoje demos um passo sumamente importante: aprendemos como é possível efetuar cálculos numéricos usando apenas circuitos digitais. E, melhor ainda: vimos que não se trata de nenhuma proeza, muito pelo contrário. Trata-se de uma tarefa perfeitamente ao alcance de nossa compreensão e baseada exclusivamente nos conhecimentos que adquirimos até agora.

Eu não disse que era fácil?

E daqui para a frente, ficará ainda mais fácil. Espere e veja se não tenho razão.