Sítio do Piropo

B. Piropo

< Coluna B. Piropo >
< (publicada no site "Fórum PCs") >

Qual é a melhor maneira de dividir um segmento de reta em duas partes?

Talvez a pergunta tenha lhe parecido um tanto estúpida. Vou tentar explicá-la melhor.

Imagine um segmento de reta de um comprimento qualquer como o da Figura 1. Vamos chamá-lo, como convém, de segmento AB.

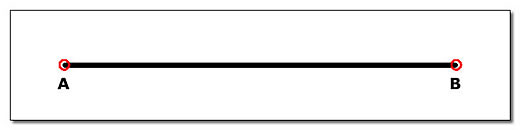
Figura 1: Segmento AB.

Ele pode ser dividido em duas partes inserindo-se em uma posição qualquer de seu interior um terceiro ponto, digamos o ponto D. Se D for inserido em um local em que as distâncias dele às duas extremidades do segmento forem iguais, ele o dividirá ao meio (ou na proporção 1:1, ou ainda "um para um"), como na Figura 2.

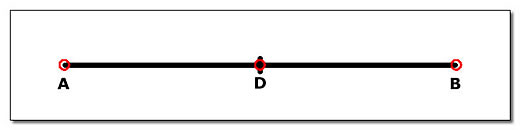
Figura 2: Segmento AB dividido ao meio.

Mas pode-se escolher qualquer outra posição para o ponto D. A figura 3 mostra situações diversas em que o ponto D divide o segmento em diferentes proporções, como 1:2 ("um para dois", no ponto D2), 1:3 ("um para três", no ponto D3), 1:4 ("um para quatro", no ponto D4) ou qualquer outra, como a mostrada pelo ponto D da Figura 3.

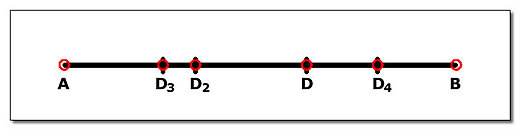
Figura 3: Segmento AB dividido em diversas proporções.

Pois bem, considerando-se tudo isto, voltemos à nossa pergunta: alguma dessas formas de dividir o segmento – ou qualquer outra, a seu critério – poderia ser considerada a melhor?

Talvez agora, que você entendeu a pergunta em toda a sua profundidade, extensão e desdobramentos, lhe advenha a certeza de que ela é realmente estúpida. Como considerar uma forma qualquer de dividir um segmento "melhor" que outra? O que se pode considerar "melhor" em um contexto como este?

Pois bem: estúpida ou não, essa questão preocupa a humanidade há milênios. Ela vem sendo discutida através dos séculos pelas mais privilegiadas mentes das gerações passadas. A história relata que esta pergunta ocupou os pensamentos de gênios do quilate de Johannes Kepler, o astrônomo que concebeu as leis do movimento planetário, Pitágoras, o mago dos números, Euclides, o pai da geometria (me refiro à euclidiana, naturalmente), Leonardo da Vinci, o gênio da ciência e das artes, e gente talvez menos ilustre mas nem por isso menos importante como Leonardo de Pisa (também conhecido como Leonardo Pisano, ou Fibonacci), que concebeu a seqüência de Fibonacci, Luca Pacioli, que dedicou todo um tratado a este tema e centenas, talvez milhares, dos mais ilustres matemáticos, geômetras, astrônomos e cientistas que abrilhantaram a história da humanidade e que acreditaram que sim, há uma forma melhor que todas as demais para dividir um segmento de reta.

Como é que pode?

E qual seria esta forma ideal de dividir um segmento, uma proporção tão especial que despertou tamanho interesse em mentes tão privilegiadas?

Esta divisão seria a correspondente à posição do ponto D na Figura 3, que define o chamado "Segmento Áureo", mostrada em destaque na Figura 4. Ela foi considerada por todos estes cérebros geniais como a forma mais bonita, mais harmônica, mais elegante, esteticamente perfeita, a mais nobre maneira de dividir um segmento de reta.

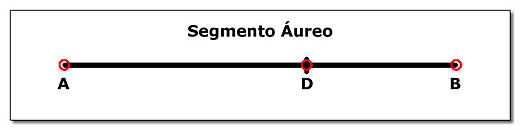
Figura 4: O segmento áureo.

Mas o que tem esta posição do ponto D que a torna tão especial? E em que proporção ela divide o segmento?

Voltemos um pouco no tempo. Caminhemos pouco mais de vinte e três séculos em direção ao passado até o ano 300 AC quando o genial Euclides publicou seus "Elementos", uma formidável coleção de treze volumes que sedimentaram as bases da chamada Geometria Euclidiana e que foram, talvez, junto com o "Philosophiae naturalis principiae mathematica" de Newton, as publicações mais importantes da ciência universal.

Euclides iniciou os "Elementos" pelos postulados, ou axiomas, verdades tão evidentes que não necessitavam (algumas delas na verdade nem poderiam) ser demonstradas. Como por exemplo o axioma que afirma que "por um ponto de um plano só se pode traçar uma reta paralela a outra reta". Em seguida, usando apenas seus axiomas, régua, compasso e lógica pura, Euclides demonstrou diversas "proposições" ou "teoremas". Por exemplo, a proposição 10 do livro 1 dos "Elementos" mostra como dividir um segmento de reta exatamente ao meio traçando duas circunferências a partir de suas extremidades e unindo as interseções destas circunferências por uma reta que, demonstrou Euclides, não somente dividia o segmento ao meio como era perpendicular a ele (veja Figura 5).

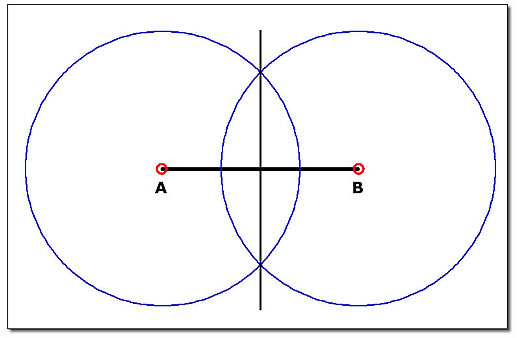
Figura 5: Divisão de um segmento ao meio
(Euclides, "Elementos", livro 1).

E assim, de teorema em teorema, Euclides criou toda uma estrutura maravilhosamente complexa e interligada de conhecimentos que hoje conhecemos por "geometria Euclidiana".

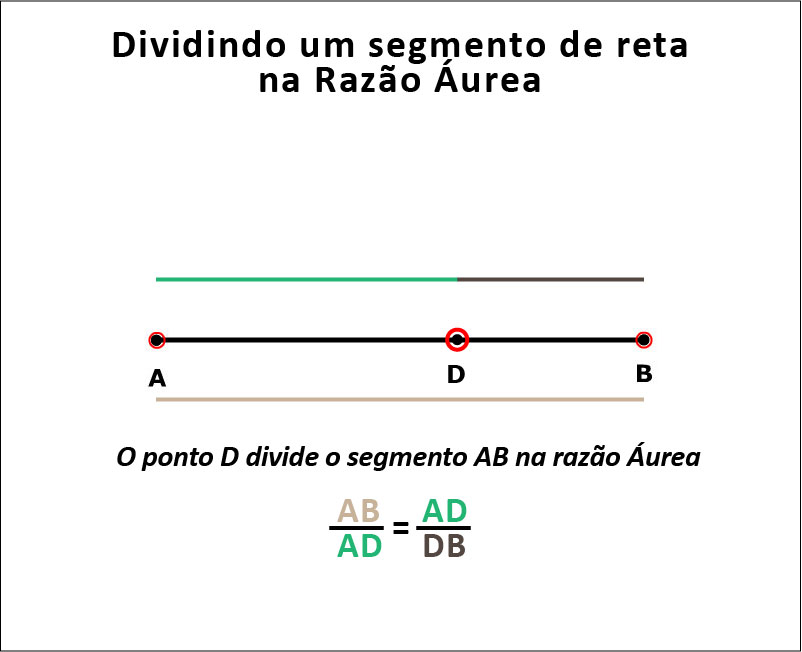
Pois bem: na proposição 30 do livro 6 de seus "Elementos" Euclides ensina como "dividir um segmento nas razões média e extrema". E esta divisão, você já deve ter adivinhado, corresponde exatamente àquela exibida na Figura 4, que define o segmento áureo (ou de ouro).

O que quis Euclides dizer quando se referiu às "razões média e extrema"? Simples: ele quis dizer que a razão (ou "proporção") existente entre o comprimento do segmento inteiro e o de sua maior divisão (razão extrema) é exatamente igual á razão (ou "proporção") entre o comprimento desta maior divisão e o da menor (razão média). E que é exatamente isto, esta dupla proporcionalidade entre apenas três elementos, que torna esta forma de dividir o segmento tão especial.

Empregando o meio usual de exprimir proporções, teremos:

AB/AD = AD/DB

Mas qual será o valor (numérico) desta proporção? Bem, não é difícil calculá-lo. Bastam algumas noções elementares de matemática, incluindo a resolução de uma equação do segundo grau, coisa que se aprende no primeiro (desculpem, mas o jogo de palavras foi irresistível...)

A solução é mostrada na Figura 6, mas se você não é chegado a matemática pode pular os entrementes e ir direto aos finalmentes logo após a figura.

Figura 6: Cálculo da Razão Áurea.

A proporção que estávamos procurando corresponde à primeira solução, cujo valor Fi (já justificaremos este estranho nome) é 1,61803 e a proporção será de 1:1,61803...

Esse número, o irracional Fi = 1,61803..., é um número muito especial sobre o qual ainda falaremos muito hoje e nas próximas colunas. Mas, antes de prosseguir, vamos ver o que é exatamente um número irracional. Trata-se de um número que não pode ser obtido pela divisão de dois números inteiros e que, quando expresso sob a forma de fração decimal, resulta em um número fracionário com uma quantidade infinita de "casas" decimais. O Prof. Ron Knott, usando o aplicativo matemático Maple, computou o valor numérico de Fi com dez mil casas decimais, que pode ser encontrado aqui: <desculpe, esta página foi removida > (e, apenas para sua informação: Fi foi o primeiro número irracional conhecido pela matemática).

Mas por que o nome "Fi"? Bem, acontece que números "importantes" têm nomes e símbolos. Você certamente conhece o mais famoso deles, o número "Pi", simbolizado pela letra grega de mesmo nome, também irracional e também representando uma proporção geométrica (entre o comprimento de uma circunferência e o de seu diâmetro). Pois nosso número, aquele que representa a proporção áurea, também recebeu um nome, que deriva igualmente de uma letra grega, a letra "Fi" (em inglês escreve-se "Phi", com o "ph" pronunciado com o som do fonema "f"). Há quem considere Pi e Fi os dois números mais importantes da matemática. A representação de ambos sob a forma das letras gregas correspondentes pode ser vista na Figura 7.

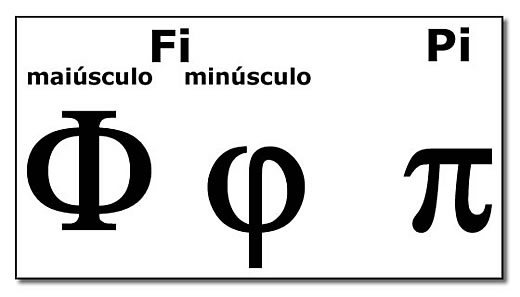
Figura 7: Representações de Fi e de Pi.

Da importância de Pi estou certo que você está ciente. E Fi, por que será tão importante? Apenas porque representa a proporção áurea? O que tem ele de tão especial?

Dá para escrever um tratado sobre isso (e de fato, em 1509 Frei Luca Bartolomeo Paciolo, matemático italiano e colaborador de Leonardo da Vinci, publicou um, intitulado "La Divina Proportione", a divina proporção, um nome alternativo pelo qual é conhecida a razão áurea). Mas vamos abordar aqui apenas alguns pontos essenciais.

Primeiro: por que "Fi"? Qual a razão de escolherem justamente esta letra grega entre tantas para representar o número correspondente à razão áurea? Consta que foi uma homenagem a < Fídias > Fídias, o famoso arquiteto e escultor grego que viveu há dois mil e quatrocentos anos mas cuja obra monumental perdura até hoje e que usava e abusava da razão áurea em suas obras. Por isso adotaram sua inicial (em grego) para dar nome ao número "Fi" que representa esta razão. E, se resta alguma dúvida sobre o fato de Fídias dedicar uma atenção especial a este número basta examinar a Figura 9, que mostra uma reprodução do frontispício original da mais célebre de suas obras, o < Partenon >, cujas ruínas (Figura 8) até hoje enfeitam o monte Olimpo, em Atenas.

Figura 8: Ruínas do Partenon, no Monte Olimpo.

Na Figura 9 estão assinaladas algumas das relações entre os elementos estruturais que obedecem à razão áurea, inclusive o retângulo que circunscreve a fachada (um "retângulo áureo", ou seja, aquele cujos lados obedecem à proporção áurea).

Figura 9: Frontispício do Partenon com razões áureas destacadas.

E por que teria Fídias recorrido tantas vezes ao número Fi?

Uma das mais importantes contribuições à ciência matemática foi dada pelos seguidores de Pitágoras que fundaram a "Escola Pitagórica", uma organização secreta de caráter religioso com 300 membros que se dedicavam ao estudo da Matemática e da Filosofia. Todas as suas ações eram orientadas por uma frase proferida por Pitágoras que afirmava: "Os números são o princípio, a fonte e a raiz de todas as coisas".

O símbolo da confraria era o pentagrama, uma estrela de cinco pontas sobre a qual voltaremos a falar mas que desde já podemos dizer que se baseia exclusivamente em combinações de segmentos de reta que obedecem à proporção áurea.

Os Pitagóricos descobriram que coisas como a harmonia musical e as relações geométricas poderiam ser expressas através de números. Disso concluíram que tudo no universo, desde os objetos físicos até fenômenos atmosféricos e o movimento dos corpos celestes era regido por números. Acreditavam que Deus era um geômetra e os números e figuras geométricas tinham natureza e poder divinos.

Cada número representava algo. Os números pares eram femininos e os ímpares, exceto "1", eram masculinos. O número 1, por ser o formador de todos os demais, representava Deus. O número 5 representava o casamento por ser a soma do primeiro número feminino (2) com o primeiro masculino (3; não esqueça que 1 não era masculino). Mas havia outros significados para os números. Por exemplo: 2, o primeiro número feminino, representava igualmente o intelecto, para gáudio das feministas. O número 3 representava o "filho", o terceiro elemento da família. E, talvez como uma prova de sua divina sabedoria, para os Pitagóricos o número 5 que representava o casamento representava igualmente a noção de "caos".

Pois bem: o que diziam os Pitagóricos do número Fi?

Sim, eles o conheciam. E além de o utilizarem fartamente na formação de seu símbolo, o pentagrama, acreditavam que seu uso conferia harmonia e beleza aos objetos. Era considerado como representante da "perfeição". Crença, aliás, compartilhada pela maioria das instituições financeiras modernas. Se duvida, meça as dimensões de seu cartão de crédito ou cartão bancário e divida a largura pela altura (em geral 8,4 cm x 5,2 cm). Se o resultado não for igual a Fi, será algo muito próximo dele (ou seja: seu cartão de crédito é um retângulo áureo, quem diria...)

Pois era por isso, por esta busca da beleza e harmonia, que Fídias dedicava tamanha atenção à proporção áurea.

Espantou-se por encontrar o número Fi em algo tão prosaico como seu cartão de crédito? Pois se espantará muito mais ao longo desta série de colunas: irá encontrá-lo nos lugares mais improváveis, de grandes obras arquitetônicas modernas, como o prédio da ONU em Nova Iorque, até conchas de moluscos, folhas de árvores e em um número imenso de famosas obras de arte. Além de espalhado, por mais que lhe custe crer, por todo o nosso corpo. Mas na coluna de hoje estamos mais interessados em suas (curiosíssimas) propriedades numéricas. Então vamos a elas.

Para começar, não deve ter lhe passado despercebido o fato da equação do segundo grau que fornece o resultado de Fi ter duas raízes. Que, calculadas, resultam em:

x = 0,61803...

e

x' = -1,61803...

Pois bem: o simétrico da segunda, como já vimos, corresponde à razão Fi e costuma ser representada pela letra Fi maiúscula. A primeira, que corresponde à relação entre os comprimentos do segmento menor e do maior, designaremos pela letra fi minúscula. Nas figuras e relações matemáticas exibidas sob a forma de ilustrações, usaremos as letras gregas correspondentes, como na Figura 10.

Figura 10: Representações de Fi e fi.

Os números Fi e fi apresentam propriedades singulares que se consubstanciam em interessantes relações numéricas das quais algumas citaremos adiante. Todas podem ser demonstradas matematicamente, mas incluir aqui sua demonstração tornaria esta coluna enfadonha. Em vez disso vou demonstrar apenas uma delas, a primeira, por ser quase evidente (e se não lhe agradarem demonstrações matemáticas, pule a figura). Quanto às demais, citarei a fonte onde encontrar a demonstração.

Como vimos na Figura 6, obtivemos o número Fi invertendo o valor da raiz positiva da equação de segundo grau. E qual era o valor daquela raiz? Era, naturalmente, o inverso de Fi. Vejamos na figura 11 qual seu valor numérico (consulte a Figura 6 se precisar):

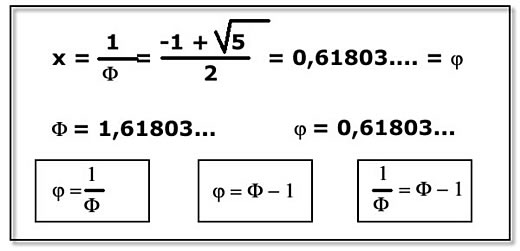
Figura 11: Algumas relações entre Fi e fi.

O número fi = 0,61803..., também chamado de "razão áurea conjugada", corresponde à raiz positiva da equação de segundo grau resolvida na Figura 6. Ele representa o inverso da razão áurea, ou seja, a razão entre os comprimentos da menor e da maior divisão do segmento (ou a relação entre o comprimento da maior divisão e o do segmento inteiro, o que dá no mesmo).

Repare nas três relações circundadas por um retângulo na parte inferior da Figura 11. A primeira significa que Fi é o inverso de fi, como demonstrado logo acima na mesma figura. A segunda é evidente por si mesma: subtraindo-se 1 de Fi obtém-se fi. Mas a terceira, que se obtém combinando as duas primeiras, ilustra uma propriedade singular, já que Fi é o único dentre os números reais positivos que a exibe: seu inverso é igual a ele mesmo menos a unidade.

As demais propriedades (ou representações de Fi) encontradas na Figura 12, algumas delas também únicas entre os números reais, podem igualmente ser demonstradas e se você se interessa por este tipo de coisa encontrará a < demonstração > na Wikipedia em espanhol (cuidado: a Wikipedia em inglês também as demonstra mas usa as letras gregas invertidas para representar as razões, ou seja, representa Fi com a letra grega minúscula e fi com a maiúscula).

Veja como são singulares e interessantes (eu não disse que Fi era um número muito especial?)

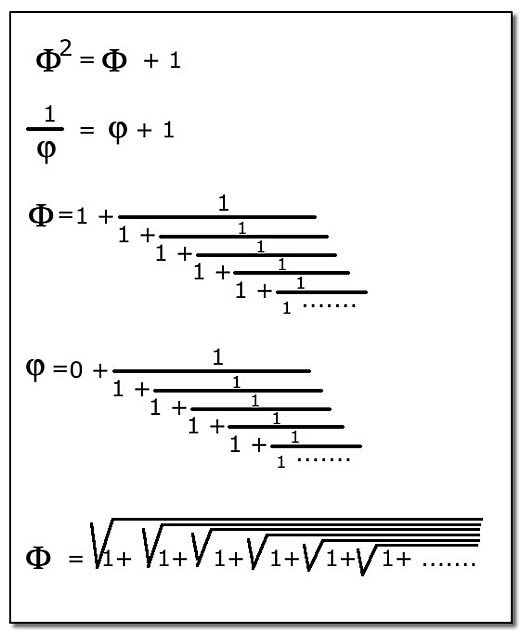
Figura 12: Relações adicionais entre Fi e Fi.

A primeira destas relações é absolutamente única: ela significa que para se obter o quadrado de Fi, basta somar uma unidade ao próprio Fi. As demais são formas alternativas e curiosas de se obter os valores numéricos de fi e Fi.

Agora, que já conhecemos tanto sobre o número Fi e a razão áurea, falta conhecer apenas uma forma de determiná-la (ou seja, de dividir um segmento na razão áurea). E se você achou que isso é muito fácil pois basta dividir o comprimento total do segmento por Fi para encontrar a maior divisão certamente esqueceu-se que Fi é um número irracional, com uma quantidade infinita de casas decimais, portanto a divisão jamais resultará em um valor exato (embora, usando-se uma representação de Fi com um número suficiente de casas decimais resulte em um valor tão aproximado que jamais poderia ser distinguido de um valor exato; mas nós aqui não nos satisfaremos com menos que o valor exato).

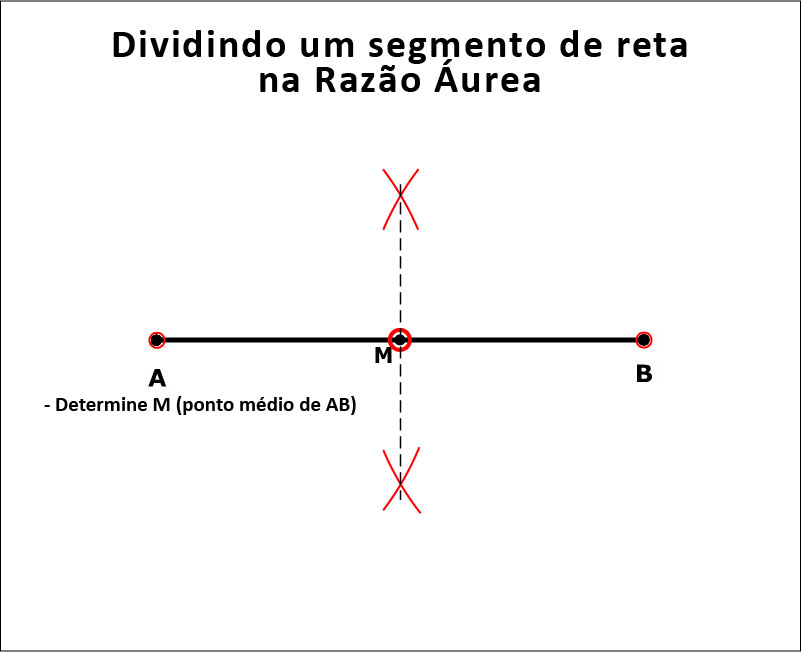
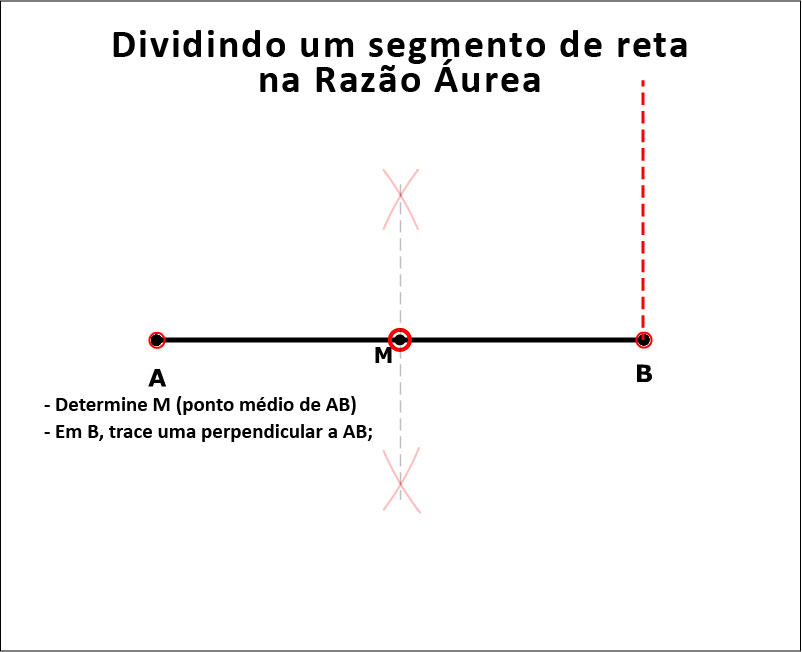
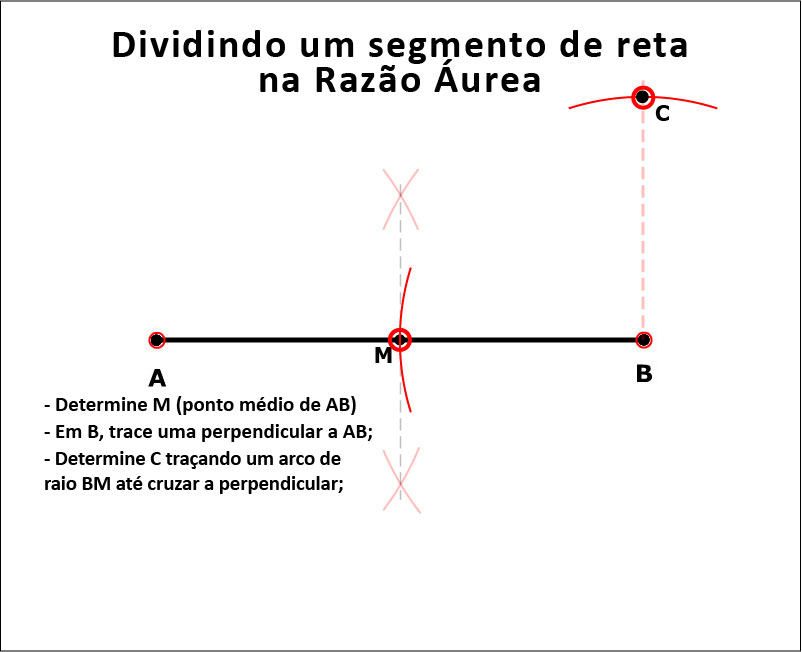
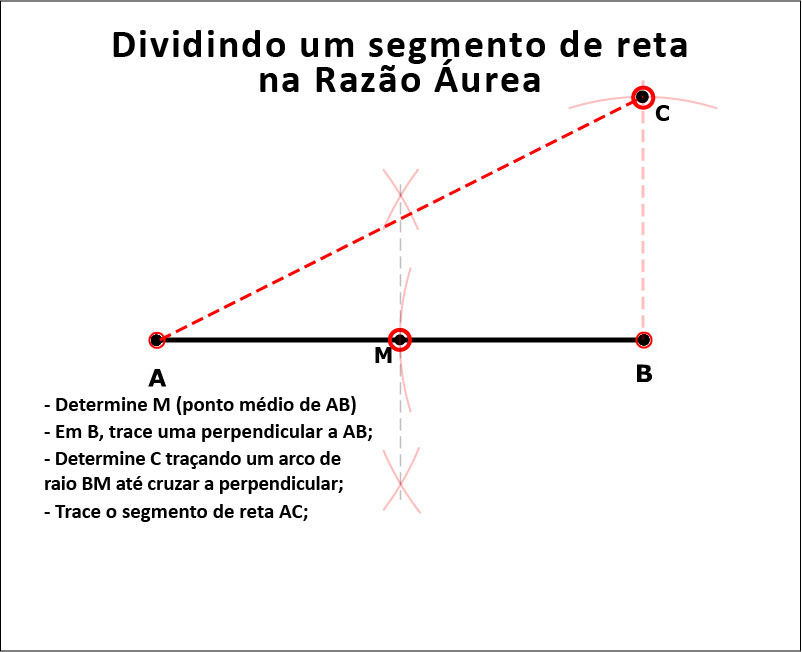
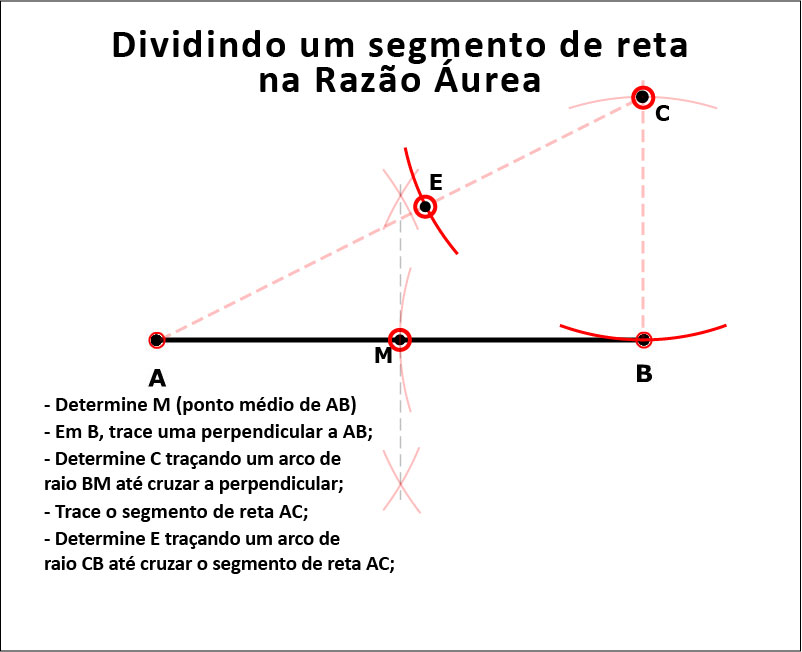
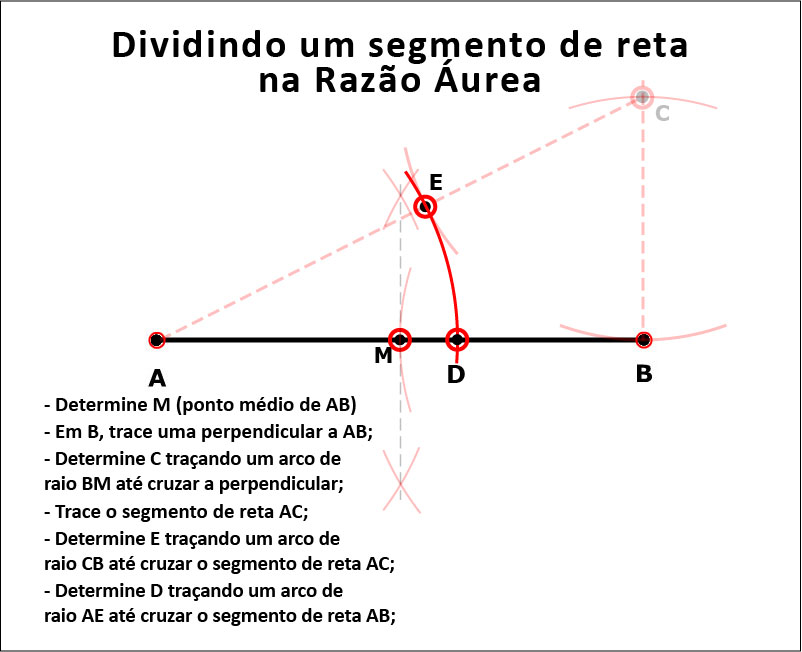
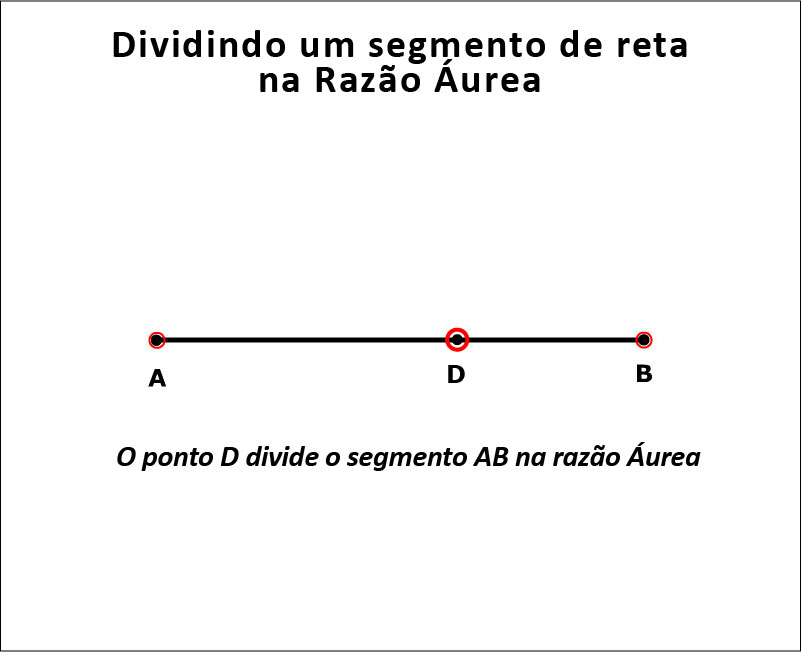
Pois aqui está a forma de fazê-lo, geometricamente. A Figura 13 mostra a construção.

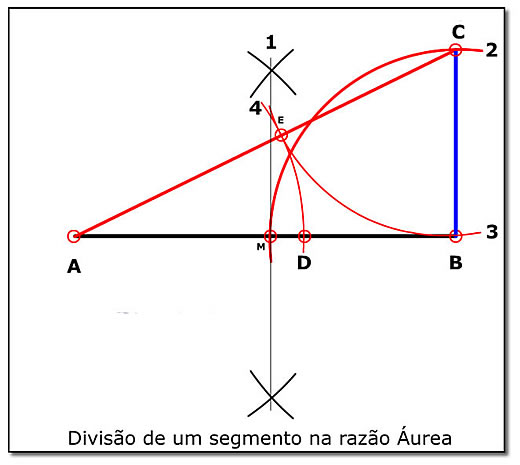
Figura 13: Como encontrar o ponto D.

E a animação mostra como fazê-lo passo a passo;

ANIMAÇÃO: Clique no botão "Seguinte" para acompanhar passo a passo a construção do diagrama anterior. Para recomeçar, clique em Início.

E se você está interessado na justificativa matemática do procedimento acima, poderá encontrar uma interessante demonstração <desculpe, esta página foi removida > aqui.

Pronto, agora você já foi apresentado ao número Fi.

Então, preparando-nos para a próxima coluna, vou lhe propor um pequeno problema. Que parece nada ter a ver com Fi, mas sempre é bom tomar cuidado com essas afirmações já que este número estranho costuma aprontar surpresas.

Mas seja lá como for, vamos ao problema. Partamos das seguintes suposições:

1) um cavalheiro adquiriu um casal de coelhos recém nascidos;

2) este (e qualquer outro) casal de coelhos demora um mês exato para atingir a maturidade, tornando-se fértil e podendo reproduzir;

3) cada casal de coelhos fértil gera um casal de filhos a cada mês, aceitando-se cruzamentos consangüíneos (é um problema de matemática, não de genética...);

4) o cavalheiro jamais se desfaz de seus coelhos que, por sua vez, nunca morrem (como eu disse, é um problema de matemática...).

Isto posto, e obedecendo-se a estas estranhas condições, pergunto: ao final de um ano quantos coelhos o cavalheiro possuirá? E quantos possuía a cada mês?

(reitero: é um problema de matemática, não uma "pegadinha" ou qualquer brincadeira parecida; o resultado será a raiz do assunto da próxima coluna e pode ser obtido exclusivamente através de raciocínio lógico baseado nas premissas acima) Quem acertar, ganha um bombom.