Sítio do Piropo

B. Piropo

< Coluna B. Piropo >
< (publicada no site "Fórum PCs") >

Esta, prometo, é a última das colunas dedicadas a questões puramente geométricas envolvendo o número Fi e a razão Áurea. Na verdade eu já deveria ter encerrado o assunto e seguido adiante, mas são tantas, tão fascinantes e, sobretudo, tão inesperadas as manifestações da razão Áurea na geometria que sempre aparece "mais um assunto que não posso deixar de mencionar" e eu continuo no tema (quem tiver paciência para ler esta coluna até o final garanto que me dará razão). Mas isso pode fazer com que esta série se torne (ainda mais) enfadonha. Nas próximas colunas discutirei apenas como a humanidade aplicou a razão Áurea em suas criações e, o que é ainda mais impressionante, como a natureza se utilizou dela para fins tão surpreendentes quanto engenhosos. Então fechemos o quesito "geometria" começando pela espiral de Fibonacci.

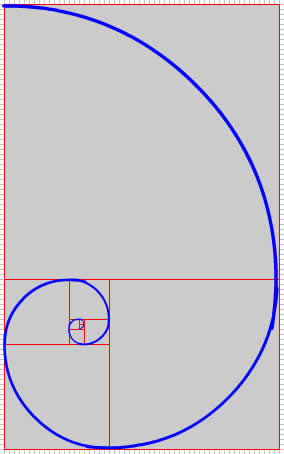
Figura 1: Espiral de Fibonacci.

A idéia básica é construir diversos quadrados com lados cujos comprimentos possam ser expressos por termos sucessivos da seqüência de Fibonacci (desprezando-se o zero inicial, naturalmente) e arrumá-los de tal forma que a união de seus vértices por uma curva produza uma linha em forma de espiral. A coisa é mais fácil de entender observando uma animação que lendo a descrição, portanto execute a animação abaixo para ver como se pode construir uma espiral de Fibonacci tomando como base uma sucessão de quadrados justapostos.

ANIMAÇÃO: Clique sucessivamente em "Siga" para executar. Ao final clique em "Início" para recomeçar.

Um meio alternativo de se obter a espiral de Fibonacci emprega triângulos Áureos, aqueles nossos conhecidos triângulos isósceles com ângulo do vértice medindo 36º. Veja como a construção gráfica é feita observando a Figura 1, onde a partir de um pequeno triângulo Áureo (preenchido em azul, no centro da espiral) foram-se construindo novos triângulos semelhantes ao primeiro (portanto sempre mantendo a razão áurea entre seus lados, pois o lado do primeiro triângulo torna-se a base do seguinte e assim por diante). A espiral é obtida unindo-se com uma curva contínua os vértices dos triângulos sucessivos. Note que os comprimentos dos lados de cada dois triângulos sucessivos se dispõem sempre na razão Áurea.

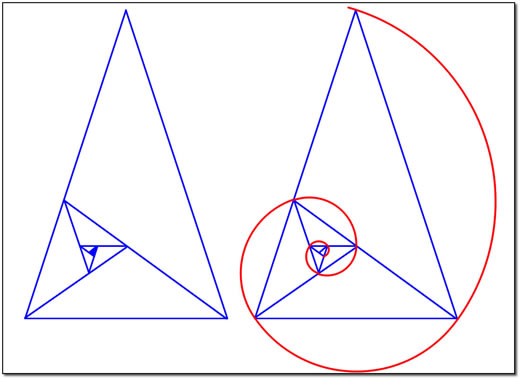
Figura 2: Espiral de Fibonacci traçada com base em triângulos Áureos.

Por enquanto deixemos a espiral de Fibonacci em paz. Voltaremos a ela mais adiante, naturalmente, mas por ora o único ponto digno de nota é que ela foi desenhada com base no número Fi, ou seja, em elementos geométricos cujas dimensões mantêm a razão Áurea. Mas quem desejar mais informações sobre ela, inclusive obter a equação de uma espiral "perfeita" (aquela que não apresenta a imprecisão inicial devida à oscilação dos valores dos quocientes de dois termos sucessivos da seqüência de Fibonacci no começo da série, mostrada na Figura 5 da terceira coluna desta série) encontrará farto material na página <desculpe, esta página foi removida da internet > "Fascinating Flat Facts about Phi" do extraordinário sítio do Prof. Ron Knott.

Agora, só para não dizerem que não falei de flores, digo, de geometria espacial ou tridimensional, vamos dedicar algum tempo aos os sólidos regulares e suas relações com o número Fi.

Um sólido, ou poliedro (do grego "pulúedros", ou "aquele que tem muitas faces") é dito "regular" quando todas as suas faces são idênticas e formadas por polígonos regulares, ou seja, que apresentam todos os lados e todos os ângulos internos iguais. O exemplo clássico é o cubo, ou hexaedro, com suas seis faces em forma de quadrados idênticos.

Não há muitos poliedros regulares. Para ser exato há apenas cinco: o tetraedro (com quatro faces formadas por triângulos eqüiláteros), o hexaedro ou cubo (com seis faces formadas por quadrados), o octaedro (com oito faces formadas por triângulos eqüiláteros), o dodecaedro (com doze faces formadas por pentágonos regulares) e o icosaedro (com vinte faces formadas por triângulos eqüiláteros). Estes poliedros regulares foram estudados por Platão quatrocentos anos antes de Cristo e por isso são conhecidos como "sólidos platônicos".

Os cinco sólidos platônicos são mostrados na Figura 3 (cuja imagem superior foi obtida em <"The Geometry Center Homepage" > e a magnífica foto que ilustra a parte inferior foi obtida no sítio < "The Creative Science Centre" > da Universidade de Sussex. Mas o que têm eles a ver com a razão Áurea?

Muito a ver. Senão, vejamos.

Figura 3: Sólidos platônicos.

Primeiro, montemos uma base, um "esqueleto" em torno dos quais construiremos nossos poliedros. A base será montada encaixando-se três retângulos Áureos, ou seja, três retângulos cujos comprimentos dos lados mantenham a razão Áurea. Se você quiser pode fazê-los em casa com pedaços de papelão ou cartolina grossa. Dois deles deverão ter no centro uma fenda com comprimento igual ao lado menor e que se estende ao longo da linha divisória paralela ao lado maior, como os retângulos amarelo e azul da Figura 4. No terceiro, para permitir o encaixe, a fenda deve se estender até um dos lados menores, como o retângulo em magenta da mesma figura. Isto feito, tudo o que precisamos para ter nossa base tridimensional é encaixar os retângulos como mostrado do lado direito da Figura 4.

Uma montagem que, aparentemente, nada tem de especial exceto pelo fato de ser formada por três retângulos Áureos idênticos.

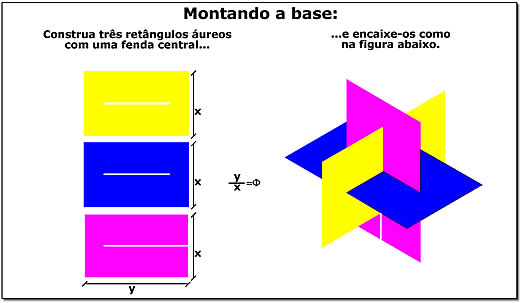
Figura 4: Base constituída por três retângulos Áureos.

E quanto aos sólidos platônicos? Bem, se você quiser construir dois deles pode fazê-lo usando nossa base.

O primeiro pode ser conseguido de forma surpreendentemente simples: use uma agulha para fazer um pequeno furo junto a cada vértice dos três retângulos e, com uma linha passando pelos furos, una cada um deles a seus vizinhos mais próximos. Agora repare o resultado: sua linha se estende em volta de toda a estrutura, formando arestas que, em conjunto, perfazem exatamente vinte triângulos eqüiláteros idênticos. "Feche" a superfície dos triângulos com papel de seda e você terá construído seu primeiro (presumo...) icosaedro regular, um dos cinco sólidos platônicos. Repare: ele está representado na imagem da esquerda da Figura 5.

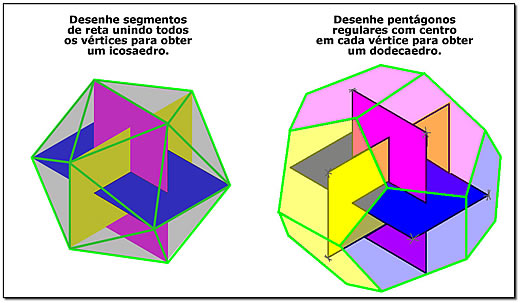
Figura 5: icosaedro (vinte faces) e dodecaedro (doze faces) regulares.

O segundo sólido platônico que pode ser obtido com nossa estrutura simples formada com os retângulos Áureos é um pouco mais complicado de se conseguir na prática, porém muito fácil de entender na teoria. Basta passar em cada vértice dos retângulos Áureos um plano perpendicular á linha que une o vértice ao centro da figura. Estes planos "cercarão" completamente a estrutura e se interceptarão. A interseção de cada dois destes planos corresponderá a uma aresta de um sólido tridimensional. Uma análise da imagem da direita da Figura 5 mostra que estas arestas formam faces pentagonais regulares (sim, retornamos ao nosso velho conhecido pentágono regular, a figura plana onde a razão Áurea se manifesta de forma mais intensa, como sabem todos os que leram a quarta coluna desta série) com os vértices dos retângulos situados em seus centros geométricos. O sólido resultante terá, portanto doze faces (os três retângulos juntos têm doze vértices e em cada um deles passa um plano). Trata-se do dodecaedro regular, outro dos sólidos platônicos. E com um pouco de imaginação, reparando bem nas duas imagens da Figura 5, você perceberá que o icosaedro da esquerda se inscreve (ou "encaixa") perfeitamente no interior do dodecaedro da direita, com os doze vértices do icosaedro coincidindo com os centros geométricos de cada face do dodecaedro (note que o icosaedro tem vinte faces e doze vértices enquanto o dodecaedro tem doze faces e vinte vértices). Um pouco mais de observação levará à conclusão que se determinarmos os pontos centrais de cada uma das vinte faces triangulares do icosaedro e os unirmos por segmentos de reta, estes segmentos formarão as arestas de um dodecaedro inscrito no icosaedro. E assim sucessivamente.

Sólidos deste tipo (ou seja, aqueles em que os centros geométricos das faces de um deles correspondem aos vértices do outro e vice-versa) chamam-se duais, ou seja, o dodecaedro é o sólido dual do icosaedro e este é o sólido dual daquele.

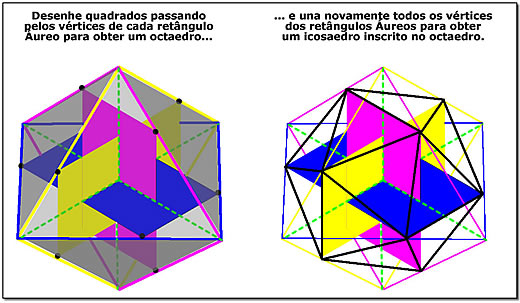
Figura 6: Octaedro e icosaedro nele inscrito.

Mas não é só isso. Examine a imagem da esquerda da Figura 6 e use bastante atenção em sua análise. Veja, no interior da figura, a mesma estrutura básica montada com os três retângulos Áureos da Figura 4. Preste atenção no retângulo azul. Note como ele é circundado por quatro linhas azuis que passam por seus vértices. Elas formam um quadrado.

Agora, repare nos outros dois retângulos Áureos, o amarelo e o magenta. Veja que tanto um quanto o outro estão igualmente circundados por quadrados desenhados com linhas da mesma cor do retângulo (amarela e magenta) e que passam por seus vértices.

Pois bem: se você se concentrar no exame da figura verá que o conjunto destas doze linhas coloridas (quatro amarelas, quatro azuis e quatro magenta) constituem as arestas de um novo sólido regular de oito faces, cada uma delas formada por um triângulo eqüilátero. Trata-se de um octaedro, o terceiro dos sólidos platônicos obtidos a partir da nossa estrutura base. E se você reparar no lado direito da Figura 6 verá que inscrito no interior deste octaedro encontra-se novamente nosso velho icosaedro, formado pela união de todos os vértices da estrutura base. Com uma novidade: seus vértices (do icosaedro) situam-se exatamente nos "pontos Áureos" (o ponto que divide o segmento na razão Áurea) de cada uma das arestas do octaedro (o que é fácil de demonstrar por semelhança de triângulos; tente).

Ainda faltam dois sólidos platônicos, o tetraedro e o hexaedro, ou cubo. Do tetraedro não há muito que dizer exceto que ele é o dual dele mesmo. Já quanto ao cubo...

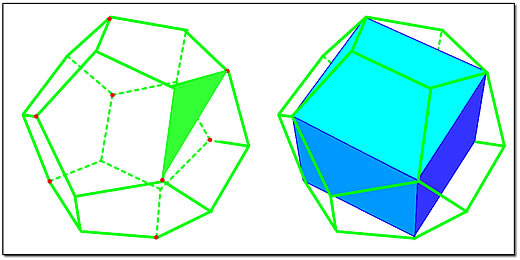
Figura 7: Hexaedro inscrito em dodecaedro.

Repare na imagem da esquerda da Figura 7. Ela representa um dodecaedro com todas as suas arestas à mostra. Veja agora os oito pontos assinalados em vermelho: tomados dois a dois eles determinam diagonais dos pentágonos regulares que formam as faces do icosaedro. Ora, se você lembrar que o ângulo interno de um pentágono é 108º, fica fácil perceber que o triângulo formado pela diagonal e pelos dois lados adjacentes que dela convergem (um destes triângulos está destacado em verde na imagem) é um triângulo Áureo obtusângulo e que seus lados e a diagonal mantêm a relação Áurea.

Pois bem: agora vamos unir os oito pontos vermelhos por segmentos de reta. Como cada um destes segmentos é uma diagonal de um dos doze pentágonos regulares idênticos que formam os lados do icosaedro, é fácil constatar que seus comprimentos são iguais. Um pouco mais de esforço e você perceberá que as diagonais formam conjuntos de linhas paralelas quatro a quatro e que se situam em ângulos retos.

Resultado: dentro no nosso dodecaedro surge o hexaedro, ou cubo, o último dos sólidos platônicos. E não é um cubo qualquer, já que o lado deste, em particular, mantém a razão Áurea com a aresta do dodecaedro.

Rapaz, não é que antes de iniciar esta série de colunas eu tinha me esquecido completamente de como o estudo da geometria euclidiana é divertido? Veja que combinação interessantíssima aparece na Figura 8, que eu encontrei em < "Polyhedron Compounds" > (um sítio que vale a visita para quem é chegado a desenhos de sólidos tridimensionais): um icosaedro dentro de um octaedro dentro de um quadrado dentro de um dodecaedro. Fuce um pouco a Figura 8, examine-a a luz dos conhecimentos de um especialista no número Fi que agora você é depois de ler estas sete colunas e tenho certeza que encontrará nela razões Áureas a dar com pau...

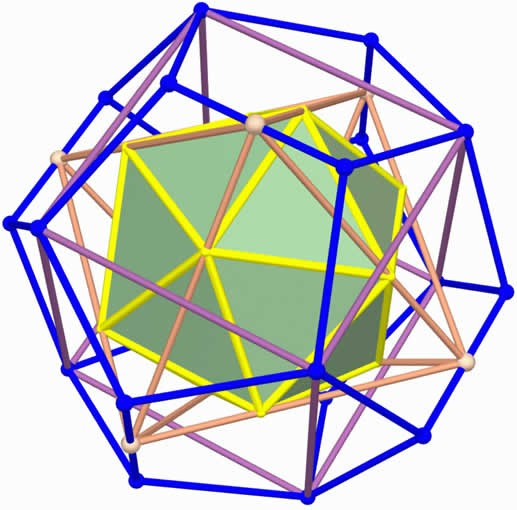
Figura 8: Quatro dos sólidos platônicos inscritos uns nos outros.

E se isso ainda não foi suficiente, faça mais uma visita ao sítio do Prof. Ron Knott e visite a página <desculpe, esta página foi removida da internet > "Phi and 3-dimensional geometry" onde você encontrará explicações mais detalhadas sobre os sólidos acima (inclusive uma lista das coordenadas de seus vértices, onde a presença do número Fi é abundante) além de outras curiosidades envolvendo o número Fi e a geometria espacial.

Pronto. Como você vê, da teoria do número Fi e da razão Áurea estamos até a tampa. Agora falta ver como ela se manifesta na prática, seja nas realizações do homem, seja na natureza.

O que faremos nas colunas finais desta série.