Sítio do Piropo

B. Piropo

< Coluna B. Piropo >
< (publicada no site "Fórum PCs") >

Na coluna anterior vimos como a natureza usa a Razão Áurea para arranjar ramos e folhas durante o crescimento das plantas. E concluímos que a razão disso é a tendência da natureza para otimizar o uso de recursos.

Mas não é apenas para isso que a Razão Áurea é usada no reino vegetal. Ela também serve para otimizar os arranjos de sementes. Senão vejamos.

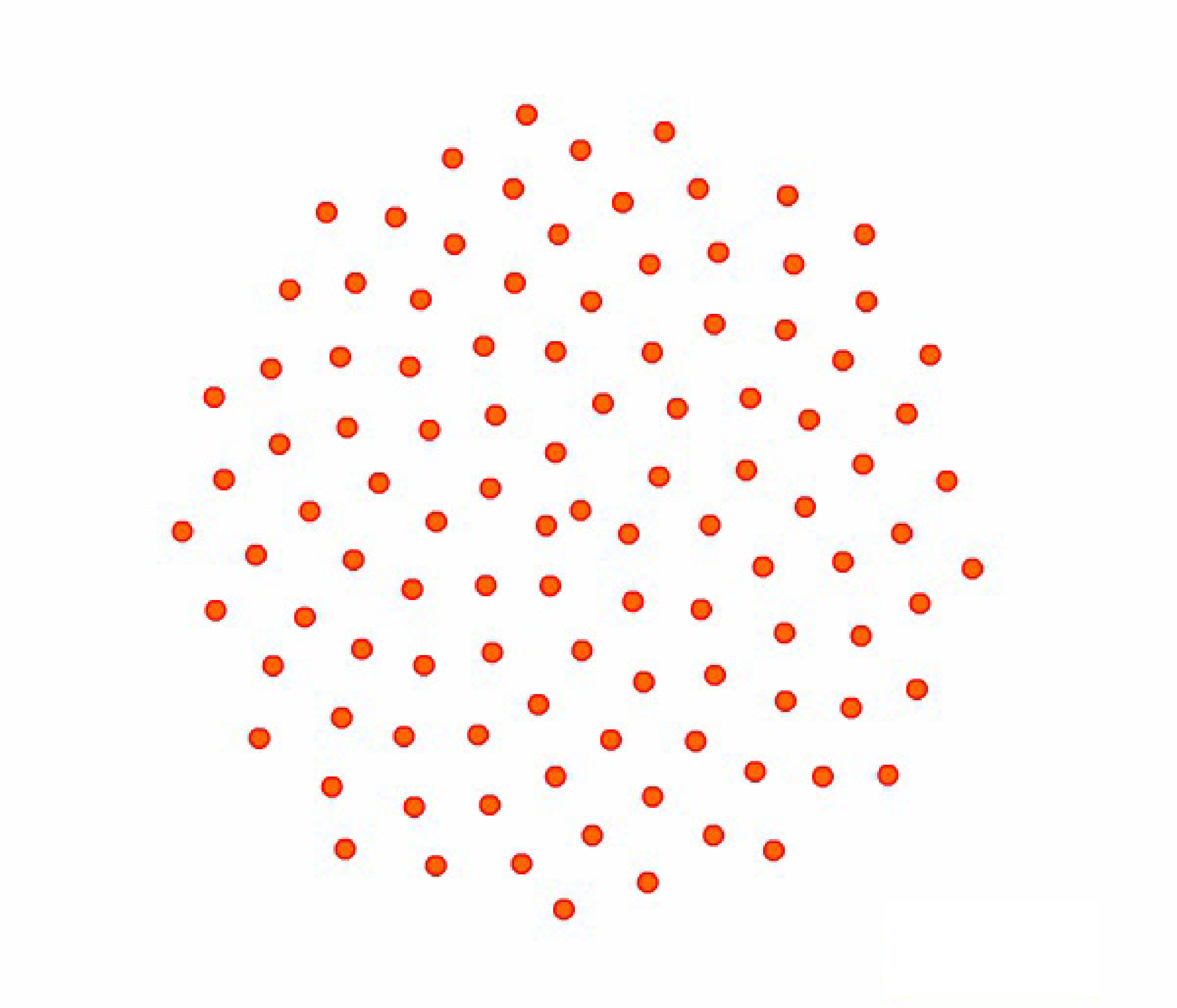
Aprecie a belíssima foto de Tim Stone obtida na página < desculpe, esta página foi removida da internet > "Fibonacci Numbers and Nature" do sítio do Prof. Ron Knott. Trata-se do centro da corola de uma Echinacea purpura, um membro da família das margaridas que medra apenas na América do Norte. Repare na distribuição de suas sementes.

Figura 1: sementes da Echinacea púrpura.

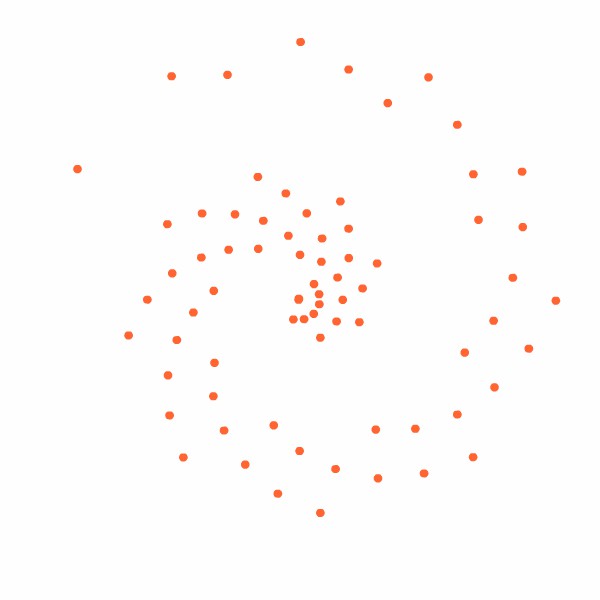
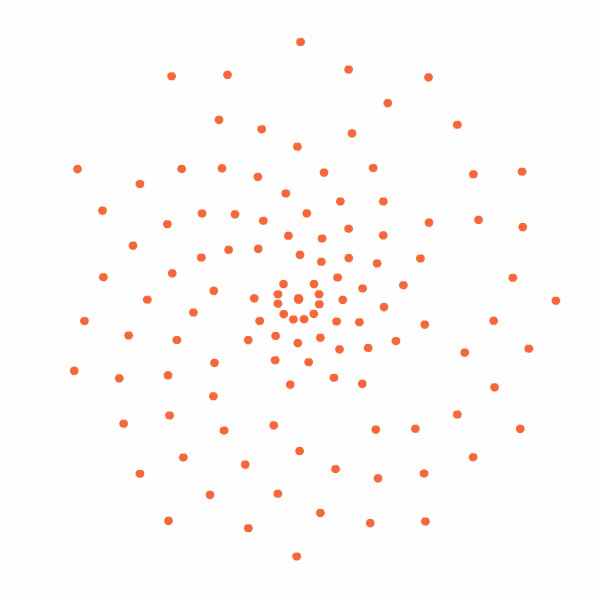
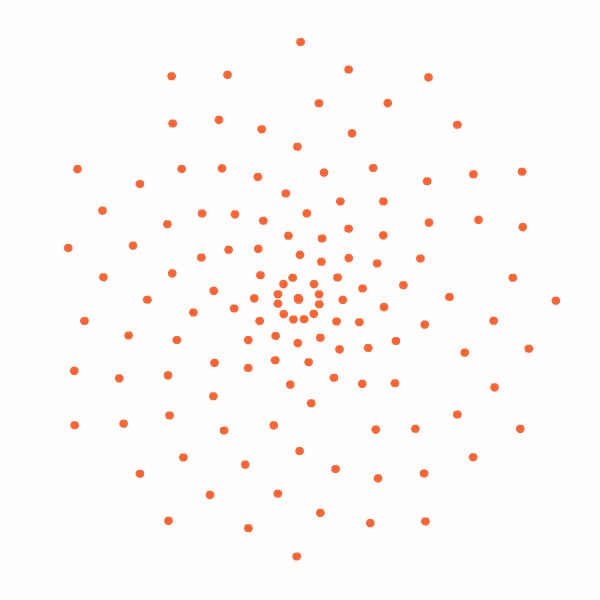
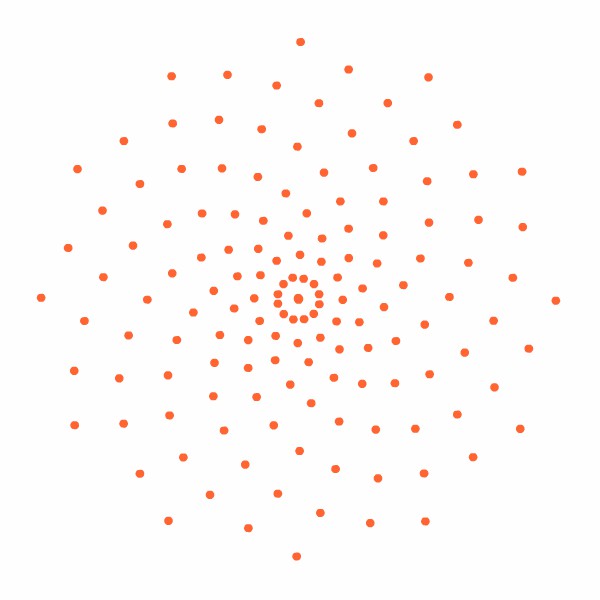
Elas se distribuem regularmente, aparentemente em circunferências concêntricas e seguindo certa lei de crescimento que faz com que o arranjo fique perfeitamente regular seja qual for seu tamanho (sim, porque as plantas crescem e vão gerando novas sementes ao longo do tempo; o "macete" da distribuição acima é que examinando-se o arranjo em qualquer época, não importa quantas sementes tenham se acumulado, ele apresentará sempre a mesma regularidade). Esquematicamente, o aspecto é parecido com o da Figura 2 (que, assim como as animações seguintes e a Figura 3, foi desenhada laboriosamente por este vosso criado).

Repare em um detalhe interessante na Figura 2: escolha um raio qualquer, uma linha reta que parta do centro em direção à periferia, e note que você jamais encontrará sementes "alinhadas" sobre ela. Curioso, não?

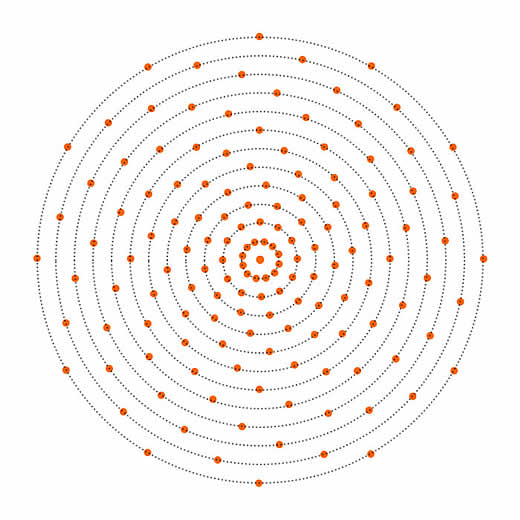
Figura 2: arranjo esquemático das sementes.

Qual teria sido a lei de formação que gerou tal arranjo? Como a natureza foi distribuindo sementes no centro das circunferências à medida que a corola crescia para a periferia?

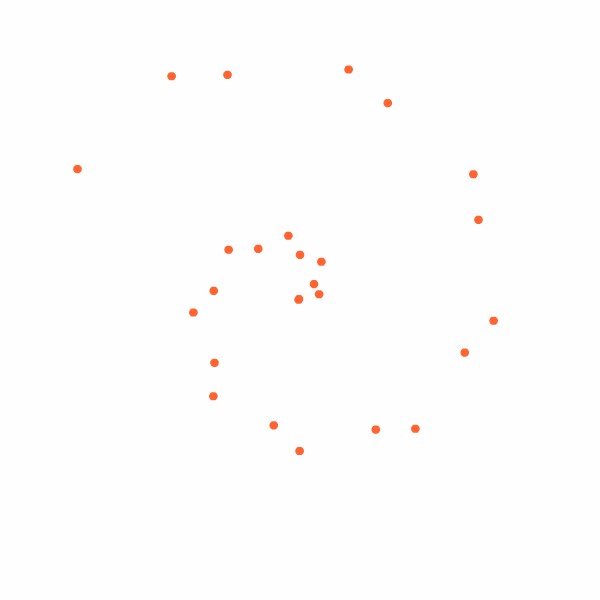
Para que possamos ter uma idéia de como esta distribuição foi criada, vamos examinar a Animação 1 (para assisti-la clique uma vez no botão "Seguinte" e ela será executada até o final; para revê-la, faça-a recomeçar clicando no botão "Início" e execute novamente um único clique em "Seguinte"). Note que o arranjo dela resultante não reproduz exatamente o exibido na figura 2 mas foi obtido usando-se a mesma lei de formação (que logo veremos qual é). Ao acompanhar a animação repare sobretudo como, embora o resultado final apresente uma certa harmonia, a distribuição de novas sementes é aparentemente anárquica, surgindo em locais inesperados e, não obstante, gerando um arranjo igualmente harmônico após cada distribuição de sementes em uma nova circunferência.

ANIMAÇÃO 1.

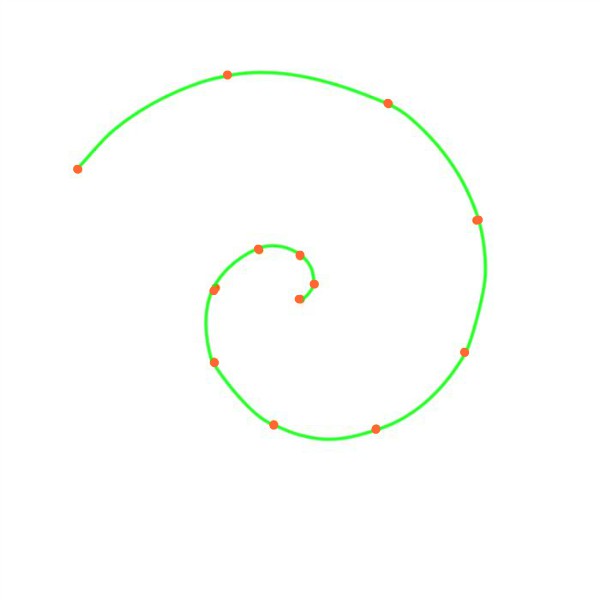
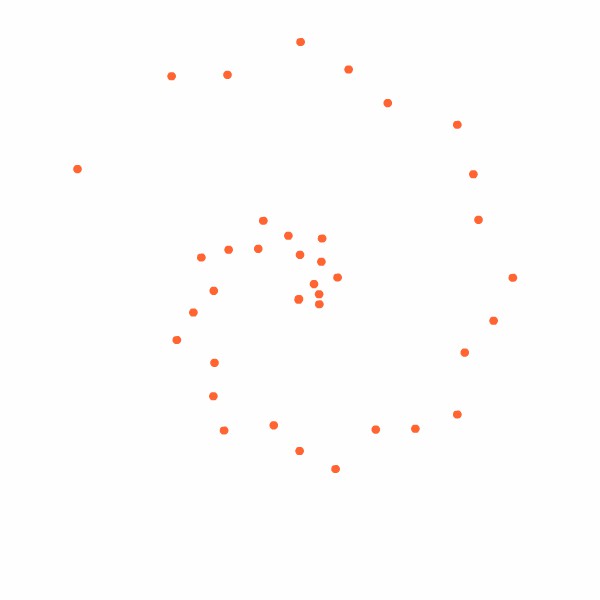
Sim, se você pensou que tudo isso tem alguma coisa a ver com Fi, não se enganou. Vamos acompanhar novamente o crescimento das sementes, porém agora de forma ordenada através da Animação 2. Ela mostra, primeiro, o modo pelo qual a natureza dispõe uma "linha" de sementes. Repare no início da animação: a partir da primeira, no centro da corola, uma nova semente é gerada na primeira circunferência em um ponto que forma um determinado ângulo com uma linha vertical arbitrária e a partir daí todas as demais sementes são dispostas exatamente neste mesmo ângulo com a anterior até a décima terceira geração, a última mostrada na animação (que, evidentemente, pode prosseguir indefinidamente). O resultado desta etapa da animação é um conjunto de treze sementes cujas posições aparentemente não têm qualquer relação umas com as outras mas que, reparando bem, acabam se dispondo rigorosamente sobre a espiral mostrada em verde, nossa conhecida espiral de Fibonacci (porque o ângulo usado para dispor cada nova semente foi justamente um arranjo baseado no ângulo de 222,492º, que configura a Razão Áurea com os 360º da volta completa da circunferência). A partir deste ponto a animação mostra novas "linhas" de sementes sendo formadas até completar todo o centro da corola. Evidentemente as linhas crescem simultaneamente e a exibição em fases sucessivas na Animação 2 visa exclusivamente facilitar a compreensão da lei de formação usada pela natureza.

ANIMAÇÃO 2.

Veja, agora, na Figura 3, um diagrama esquemático mostrando o mesmo arranjo da Figura 2, porém com a espiral de Fibonacci assinalada. Repare como todas as demais sementes se distribuem igualmente sobre outras tantas espirais de Fibonacci de mesmo sentido que a primeira (com alguma sensibilidade e muita atenção você encontrará espirais também no sentido oposto). Veja se não é impressionante como, usando um artifício tão simples como girar sempre um ângulo de Fi radianos para situar a semente na circunferência seguinte, a natureza conseguiu criar uma distribuição que é ao mesmo tempo singela e altamente sofisticada (no sítio do Prof. Knott você encontrará diversas animações demonstrando alguns arranjos possíveis onde se pode variar o ângulo de distribuição de sementes e o diâmetro das circunferências sucessivas dos quais se pode concluir que o arranjo ótimo se obtém sempre usando o ângulo de 222,492º ou seu complemento, 137,508º, o que dá no mesmo).

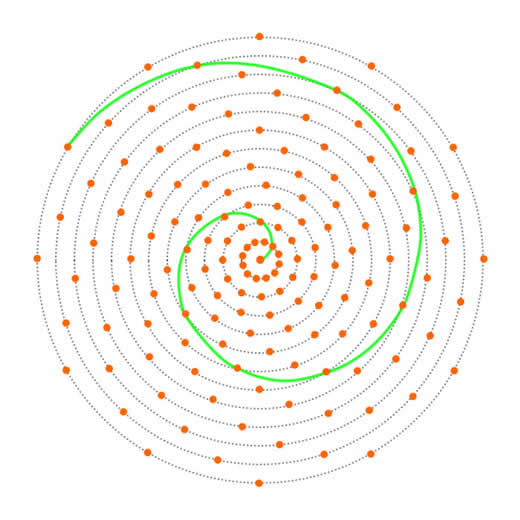
Figura 3: Distribuição de sementes e espiral de Fibonacci.

Tudo isto não é apenas uma divagação teórica. É efetivamente um artifício usado pela natureza para distribuir sementes no centro de corolas de flores, pétalas nas próprias flores, "gomos" em vegetais e outras tantas coisas que tais. Para termos certeza, verifiquemos alguns exemplos práticos, todos obtidos da Internet.

Figura 4: Sementes de girassol.

Veja, na figura 4, como as sementes se distribuem exatamente conforme esta lei de geração no centro da corola de flores de girassol.

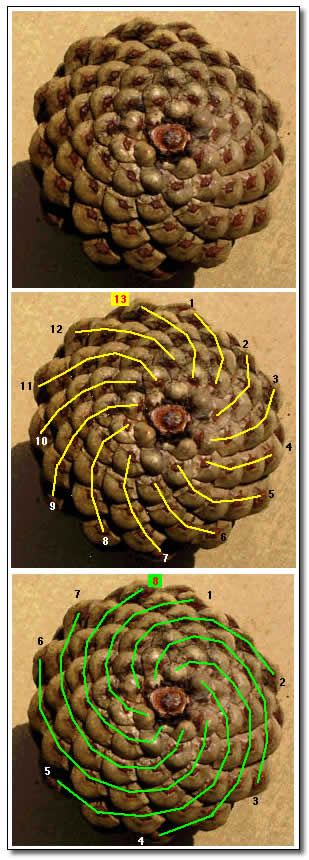
Figura 5: fruto do pinheiro.

Mas não são apenas as sementes internas. Veja, na Figura 5 (todas as três imagens obtidas no sítio do Prof. Ron Knott) a mesma foto tirada do fruto de um pinhão, do lado do "talo" (através do qual ele é originalmente preso à árvore) e repare como seus "gomos" se distribuem de forma espiralada, podendo-se contar 8 espirais em um sentido e 13 em outro (como sabemos, 8 e 13 são dois números sucessivos da seqüência de Fibonacci).

Figura 6: couve-flor e brócolis.

Veja agora na Figura 6 como, com alguma atenção (e uma dose não desprezível de imaginação, sou obrigado a admitir), até mesmo nos prosaicos legumes couve-flor e brócolis (figuras obtidas igualmente no sítio do Prof Ron Knott) se podem encontrar exemplos de espirais de Fibonacci. E, da próxima vez que se preparar para descascar um abacaxi ou comer uma fruta-do-conde, não se esqueça de olhar para os frutos na direção de seu eixo e reparar nas espirais.

Também as pétalas das flores têm algo a ver com o nosso velho conhecido Fi.

Figura 7: Flor de maracujá.

Veja, na Figura 7, duas fotos da mesma flor de maracujá (Passiflora incarnata) tiradas de ângulos opostos. Veja do lado esquerdo uma seqüência de três folhas seguidas de cinco folhas e mais cinco folhas em ângulo com estas. Veja do lado direito um conjunto de 5 estames (em forma de "T"), abaixo de três carpelos roxos e acima de cinco folhas verdes. As dez folhas que aparecem cercando o conjunto são os mesmos dois conjuntos de cinco folhas mostrados por baixo na foto da esquerda. Tanto 3 quanto 5 são números de Fibonacci. E repare no conjunto de estames bicolores (branco e púrpura). Eu não os contei, mas aposto que se algum de vocês tiver paciência suficiente para fazê-lo encontrará mais um número de Fibonacci.

Mas não é só isso, há mais. Por exemplo: por que são tão raros os trevos de quatro folhas?

Bem, é que o número de pétalas das flores também costuma obedecer à seqüência de Fibonacci. O Sítio do Prof. Knott lista flores com 3, 5, 8, 13, 21, 34, 55 e 89 pétalas, todos números de Fibonacci.

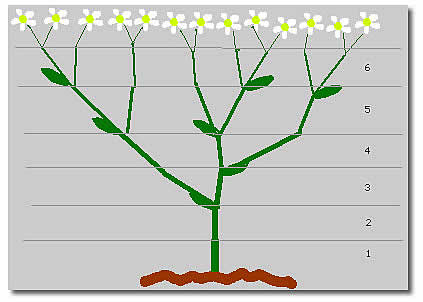
Figura 8: Mil-folhas (esquema).

Finalmente, no que toca a plantas, veja na Figura 8 um diagrama esquemático que mostra o desenvolvimento de um exemplar de "Mil folhas" (Achillea ptarmica). Ela apresenta uma taxa de crescimento segundo a qual novos ramos são liberados a intervalos regulares. Supondo que o ramo "recém-nascido" precisa crescer durante algum tempo (digamos, dois meses) para adquirir robustez suficiente para suportar novos ramos e imaginando que a partir deste ponto, após a floração, cada ramo se bifurque mensalmente, depois de alguns meses teremos, a cada mês, exatamente a disposição mostrada na Figura 8, onde o número de ramos (1; 1; 2; 3; 5; 8; 13 e assim por diante) replica exatamente a seqüência de Fibonacci.

No que diz respeito ao reino vegetal, isto é tudo o que me ocorre sobre Fi.

O que falta?

Falamos de Pi nas artes, nas ciências, no mundo animal e vegetal, falar mais em que?

Bem, no que toca ao reino animal, faltou mencionar uma espécie em particular, um predador notável, a única espécie capaz de alterar a natureza e que, apesar disso, estranhamente, não o faz em seu próprio benefício. Muito pelo contrário, vem usando esta extraordinária capacidade para, pouco a pouco, tornar o planeta inabitável para ela mesma. O mais surpreendente é que ela outorgou a si mesma o título de "superior" às demais e se diz ser a única espécie racional. Trata-se de uma subespécie de primata, o animal peculiar retratado na Figura 9 (obtida da Wikipedia), que responde (um tanto indevidamente) pelo nome científico de Homo sapiens.

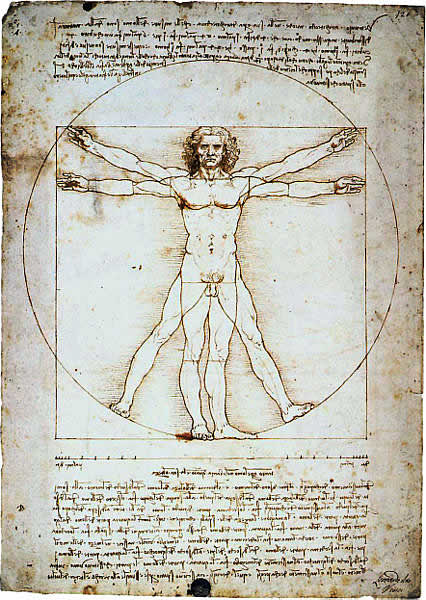
Figura 9: Vitruvian Man, desenho de Da Vinci.

A figura, mundialmente conhecida como "Homem Vitruviano" por ter Da Vinci para desenhá-la se baseado em um estudo do arquiteto romano Marcus Vitruvius sobre proporções humanas, é belíssima. Nela o umbigo representa o centro do corpo humano que pode ser inscrito tanto em uma circunferência quanto em um retângulo. Diz Da Vinci textualmente no documento acima representado (que, curiosamente, foi grafado em escrita especular, ou seja, "ao contrário", de tal forma que para ser lido é necessário pô-lo em frente a um espelho, um recurso usado freqüentemente por Da Vinci e que dependia de uma extraordinária destreza para escrever):

"The navel is naturally placed in the centre of the human body, and, if in a man lying with his face upward, and his hands and feet extended, from his navel as the centre, a circle be described, it will touch his fingers and toes. It is not alone by a circle, that the human body is thus circumscribed, as may be seen by placing it within a square. For measuring from the feet to the crown of the head, and then across the arms fully extended, we find the latter measure equal to the former; so that lines at right angles to each other, enclosing the figure, will form a square".

"O umbigo é naturalmente colocado no centro do corpo humano e, se em um homem deitado com o rosto para cima e as mãos e os pés estendidos, for traçada uma circunferência tendo o umbigo como centro, ele tocará seus dedos das mãos e dos pés. Não é só por uma circunferência que o corpo humano é assim circunscrito, como pode ser visto ao colocá-lo dentro de um quadrado. A medida dos pés ao topo da cabeça é igual à dos braços totalmente estendidos, de modo que as linhas perpendiculares entre si, envolvendo a figura, formarão um quadrado".

Porém o mais extraordinário fato que a cuidadosa observação da figura evidencia é a enorme quantidade de "Razões Áureas" existentes entre as medidas da figura.

Procure-as você mesmo. E, se encontrar alguma dificuldade para achá-las, sugiro duas fontes: a página <"The Human Body" > e o interessante livro de Dan Brown, "O Código Da Vinci".

Mesmo porque foi justamente o texto de Brown sobre o número Fi neste último livro que despertou minha atenção para o assunto e me levou a escrever esta longa, longa, longa série de colunas sobre tão fascinante número.

Que, aliás, termina aqui.

Semana que vem, afinal, voltaremos a discutir informática.